
分析 (Ⅰ)求出函數的導數,通過討論a的范圍,求出函數的單調區間即可;
(Ⅱ)設F(x)=f(x)-f($\frac{2}{a}$-x),根據函數的單調性求出不等式的解集即可;
(Ⅲ)求出a>0,不妨設0<x1<$\frac{1}{a}$<x2,則$\frac{2}{a}$-x1∈($\frac{1}{a}$,+∞),根據函數的單調性得到f(x1)<f($\frac{2}{a}$-x1),由f(x1)=f(x2),替換即可.
解答 解:(I)f(x)的定義域為(0,+∞),
f′(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
(1)當a≤0時,恒有f′(x)>0,故f(x)在(0,+∞)上單調遞增;
(2)當a>0時,由f′(x)>0,得0<x<$\frac{1}{a}$,
故f(x)在(0,$\frac{1}{a}$)上單調遞增,在($\frac{1}{a}$,+∞)上單調遞減,
綜上(1)(2)可知:當a≤0時,f(x)的單調遞增區間為(0,+∞);
當a>0時,f(x)的單調遞增區間為(0,$\frac{1}{a}$),單調遞減區間為($\frac{1}{a}$,+∞);
(II)f(x)的定義域為(0,+∞),所以x>0,且$\frac{2}{a}$-x>0,而a>0,0<x<$\frac{2}{a}$;
設F(x)=f(x)-f($\frac{2}{a}$-x)=lnx-ax-ln($\frac{2}{a}$-x)+a($\frac{2}{a}$-x)=lnx=ln($\frac{2}{a}$-x)-2ax+2,
F′(x)=$\frac{2{a(x-\frac{1}{a})}^{2}}{x(\frac{2}{a}-x)}$≥0,且當且僅當x=$\frac{1}{a}$時取等號,
所以F(x)在(0,$\frac{2}{a}$)上單調遞增,又因為x=$\frac{1}{a}$時,F(x)=F($\frac{1}{a}$)=0,
所以當x∈(0,$\frac{1}{a}$)時,F(x)<0,當x∈($\frac{1}{a}$,$\frac{2}{a}$)時,F(x)>0,
故f(x)-f($\frac{2}{a}$-x)>0的解集為($\frac{1}{a}$,$\frac{2}{a}$);
(III)由(I)知a≤0時,f(x)在(0,+∞)上單調遞增,若f(x1)=f(x2),
則x1=x2不合題意;
故a>0,而f(x)在(0,$\frac{1}{a}$)上單調遞增,在($\frac{1}{a}$,+∞)上單調遞減,
若存在兩個不相等的正數x1,x2滿足f(x1)=f(x2),
則x1,x2必有一個在(0,$\frac{1}{a}$)上,另一個在($\frac{1}{a}$,+∞),
不妨設0<x1<$\frac{1}{a}$<x2,則$\frac{2}{a}$-x1∈($\frac{1}{a}$,+∞),
又由(II)知x∈(0,$\frac{1}{a}$)時,F(x)<0,即f(x)-f($\frac{2}{a}$-x)<0,
所以f(x1)<f($\frac{2}{a}$-x1),
因為f(x1)=f(x2),所以f(x2)<f($\frac{2}{a}$-x1),
又因為f(x)在($\frac{1}{a}$,+∞)上單調遞減,所以x2>$\frac{2}{a}$-x1,
即 x1+x2>$\frac{2}{a}$.
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及分類討論思想,轉化思想,是一道綜合題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖所示,一個圓柱形乒乓球筒,高為20厘米,底面半徑為2厘米.球筒的上底和下底分別粘有一個乒乓球,乒乓球與球筒底面及側面均相切(球筒和乒乓球厚度均忽略不計).一個平面與兩個乒乓球均相切,且此平面截球筒邊緣所得的圖形為一個橢圓,則該橢圓的離心率為$\frac{\sqrt{15}}{4}$.
如圖所示,一個圓柱形乒乓球筒,高為20厘米,底面半徑為2厘米.球筒的上底和下底分別粘有一個乒乓球,乒乓球與球筒底面及側面均相切(球筒和乒乓球厚度均忽略不計).一個平面與兩個乒乓球均相切,且此平面截球筒邊緣所得的圖形為一個橢圓,則該橢圓的離心率為$\frac{\sqrt{15}}{4}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
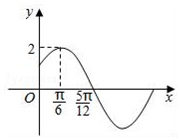 已知函數f(x)=Asin(ωx+φ)
已知函數f(x)=Asin(ωx+φ)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com