
分析 (1)用輾轉相除法求840與1764的最大公約數,寫出1764=840×2+84,840=84×10+0,得到兩個數字的最大公約數.
(2)利用累加權重法,即可將七進制數轉化為十進制,利用除K取余法即可將十進制數轉化為八進制數.
解答 解:(1)用輾轉相除法求840與1764的最大公約數.
1764=840×2+84,
840=84×10+0
∴840與1764的最大公約數是84.
(2)由題意,666(7)=6×72+6×71+6×70=342(10),
342÷8=42…6
42÷8=5…2
5÷8=0…5
可得:342(10)化成8進制是526(8).
點評 本題考查進制之間的轉化,考查輾轉相除法和更相減損術,熟練掌握進制之間的轉化法則是解題的關鍵,這屬于算法案例中的一種題目,解題時需要有耐心,認真計算,不要在數字運算上出錯,本題是一個基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | -6 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
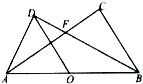 如圖,△ABC與△ABD都是以AB為斜邊的直角三角形,O為線段AB上一點,BD平分∠ABC,且OD∥BC.
如圖,△ABC與△ABD都是以AB為斜邊的直角三角形,O為線段AB上一點,BD平分∠ABC,且OD∥BC.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 100 | B. | 101 | C. | 50 | D. | 51 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-∞,\frac{{\sqrt{e}}}{e}-8]$ | B. | $[\frac{{\sqrt{e}}}{e}-8,+∞)$ | C. | $[\sqrt{2},e)$ | D. | $(-\frac{{\sqrt{3}}}{3},\frac{e}{2}]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2<x<2 | B. | x>2或-2<x<0 | C. | -2<x<0 | D. | x<-2或x>2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com