
【題目】已知函數f(x)=(x﹣a)cosx﹣sinx,g(x)![]() x3
x3![]() ax2,a∈R
ax2,a∈R
(1)當a=1時,求函數y=f(x)在區間(0,![]() )上零點的個數;
)上零點的個數;
(2)令F(x)=f(x)+g(x),試討論函數y=F(x)極值點的個數.
【答案】(1)零點的個數為0,(2)無極值.
【解析】
(1)結合函數![]() 的單調性和極值,即可得到本題答案;
的單調性和極值,即可得到本題答案;
(2)先求導,再分類討論,即可得到![]() 的單調區間和極值,由此即可得到本題答案.
的單調區間和極值,由此即可得到本題答案.
(1)當![]() 時,
時,![]() ,
,
∴![]() ,
,
因為當![]() 時,
時,![]() ,
,
所以當![]() 時,
時,![]() ,
,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,函數取得最大值
時,函數取得最大值![]() ,
,
所以函數![]() 在區間
在區間![]() 上零點的個數為0;
上零點的個數為0;
(2)![]() ,
,
![]() ,
,
令![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上為增函數,又
上為增函數,又![]() ,
,
所以當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() .
.
①若![]() 時,
時,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞減,
上單調遞減,
故有2個極值;
②若![]() 時,
時,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞減,
上單調遞減,
故有2個極值點;
③當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() 在R上單調遞增,無極值點.
在R上單調遞增,無極值點.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】為了了解一個小水庫中養殖的魚的有關情況,從這個水庫中多個不同位置捕撈出100條魚,稱得每條魚的質量(單位:kg),并將所得數據分組,畫出頻率分布直方圖(如圖所示).
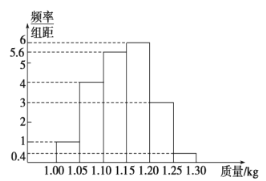
(1)在下面表格中填寫相應的頻率;
分組 | 頻率 |
| |
| |
| |
| |
| |
|
(2)估計數據落在![]() 中的概率;
中的概率;
(3)將上面捕撈的100條魚分別作一記分組頻率號后再放回水庫.幾天后再從水庫的多處不同位置捕撈出120條魚,其中帶有記號的魚有6條.請根據這一情況來估計該水庫中魚的總條數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場為改進服務質量,在進場購物的顧客中隨機抽取了![]() 人進行問卷調查.調查后,就顧客“購物體驗”的滿意度統計如下:
人進行問卷調查.調查后,就顧客“購物體驗”的滿意度統計如下:
滿意 | 不滿意 | |
男 |
|
|
女 |
|
|
![]() 是否有
是否有![]() 的把握認為顧客購物體驗的滿意度與性別有關?
的把握認為顧客購物體驗的滿意度與性別有關?
![]() 若在購物體驗滿意的問卷顧客中按照性別分層抽取了
若在購物體驗滿意的問卷顧客中按照性別分層抽取了![]() 人發放價值
人發放價值![]() 元的購物券.若在獲得了
元的購物券.若在獲得了![]() 元購物券的
元購物券的![]() 人中隨機抽取
人中隨機抽取![]() 人贈其紀念品,求獲得紀念品的
人贈其紀念品,求獲得紀念品的![]() 人中僅有
人中僅有![]() 人是女顧客的概率.
人是女顧客的概率.
附表及公式: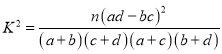 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,過原點O且斜率不為0的直線與橢圓C交于P,Q兩點.
,過原點O且斜率不為0的直線與橢圓C交于P,Q兩點.
(1)若![]() 為橢圓C的一個焦點,求橢圓C的標準方程;
為橢圓C的一個焦點,求橢圓C的標準方程;
(2)若經過橢圓C的右焦點的直線l與橢圓C交于A,B兩點,四邊形OAPB能否為平行四邊形?若能,求此時直線OP的方程,若不能,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校共有教職工900人,分成三個批次進行繼續教育培訓,在三個批次中男、女教職工人數如下表所示. 已知在全體教職工中隨機抽取1名,抽到第二批次中女教職工的概率是0.16 .

(1)求![]() 的值;
的值;
(2)現用分層抽樣的方法在全體教職工中抽取54名做培訓效果的調查, 問應在第三批次中抽取教職工多少名?
(3)已知![]() ,求第三批次中女教職工比男教職工多的概率.
,求第三批次中女教職工比男教職工多的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com