
【題目】某學校共有教職工900人,分成三個批次進行繼續教育培訓,在三個批次中男、女教職工人數如下表所示. 已知在全體教職工中隨機抽取1名,抽到第二批次中女教職工的概率是0.16 .

(1)求![]() 的值;
的值;
(2)現用分層抽樣的方法在全體教職工中抽取54名做培訓效果的調查, 問應在第三批次中抽取教職工多少名?
(3)已知![]() ,求第三批次中女教職工比男教職工多的概率.
,求第三批次中女教職工比男教職工多的概率.
【答案】(1)144(2)12(3)![]()
【解析】
第一問中利用等概率抽樣求解樣本容量.可知由![]() ,解得
,解得![]()
第二問中,由于用分層抽樣的方法在全體教職工中抽取54名做培訓效果的調查
因此先求第三批的人數,然后按比例抽樣得到第三批中抽取的人數
第三問中,結合古典概型概率公式求解得到.
解: (1)由![]() ,解得
,解得![]() . ……………3分
. ……………3分
(2)第三批次的人數為![]() ,
,
設應在第三批次中抽取![]() 名,則
名,則![]() ,解得
,解得![]() .
.
∴應在第三批次中抽取12名. ……………6分
(3)設第三批次中女教職工比男教職工多的事件為![]() ,第三批次女教職工和男教職工數記為數對
,第三批次女教職工和男教職工數記為數對![]() ,
,
由(2)知![]() ,則基本事件總數有:
,則基本事件總數有:
![]()
![]() ,共9個,
,共9個,
而事件![]() 包含的基本事件有:
包含的基本事件有:![]()
![]() 共4個,
共4個,
∴![]() . ……………………………………12分
. ……………………………………12分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
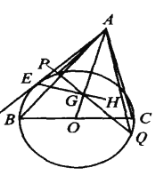
【題目】如圖,設H為銳角△ABC的垂心.由頂點A向以BC為直徑的⊙O作一條切線AE,切點為E,聯結EH交AO于點G,過G任意作⊙O的一條弦PQ.證明:AO 平分∠PAQ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩個人獨立地破譯一個密碼,他們能譯出密碼的概率分別為![]() 和
和![]() .
.
(1)求2個人都譯出密碼的概率;
(2)求2個人都譯不出密碼的概率;
(3)求至多1個人都譯出密碼的概率;
(4)求至少1個人都譯出密碼的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A,B,C所對邊分別為a、b、c,且2acosC=2b-c.
(1)求角A的大小;
(2)若AB=3,AC邊上的中線SD的長為![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某中學舉行的電腦知識競賽中,將高一年級兩個班參賽的學生成績進行整理后分成五組,繪制如圖所示的頻率分布直方圖.已知圖中從左到右的第一,第三,第四,第五小組的頻率分別是0.30,0.15,0.10,0.05,第二小組的頻數是40.
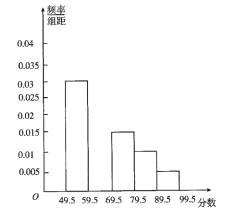
(1)補齊圖中頻率分布直方圖,并求這兩個班參賽學生的總人數;
(2)利用頻率分布直方圖,估算本次比賽學生成績的平均數和中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地某高中2018年的高考考生人數是2015年高考考生人數的1.5倍.為了更好地對比該校考生的升學情況,統計了該校2015和2018年高考情況,得到如下餅圖:

2018年與2015年比較,下列結論正確的是( )
A. 一本達線人數減少
B. 二本達線人數增加了0.5倍
C. 藝體達線人數相同
D. 不上線的人數有所增加
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com