
【題目】已知![]() (其中
(其中![]() ,
,![]() 是自然對數的底數).
是自然對數的底數).
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若不等式![]() 對于
對于![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)函數![]() 的減區間為
的減區間為![]() ,增區間為
,增區間為![]() (2)
(2)![]()
【解析】
(1)對函數求導,通過導函數的不等式確定原函數的增減區間,即可得函數![]() 的單調區間.
的單調區間.
(2)將所要證明的式子變形,建立一個函數,求導后再建立一個新的函數,再求導.需要用到兩次求導,通過最值確定正負號,再來確定原函數的單調性,通過單調性即可得到實數![]() 的取值范圍.
的取值范圍.
(1)當![]() 時,
時,![]() ,所以
,所以![]() ,
,
由![]() 得,
得,![]() ,
,![]() 得,
得,![]() ,
,
所以函數![]() 的減區間為
的減區間為![]() ,增區間為
,增區間為![]() .
.
(2)由題意![]() 對于
對于![]() 恒成立,
恒成立,
即![]() 等價于對于
等價于對于![]() 恒成立,
恒成立,
設![]() ,則由
,則由![]() 得,
得,![]() ,
,
當0<x<![]() 時,g′(x)<0,g(x)單調遞減,
時,g′(x)<0,g(x)單調遞減,
當![]() <x時,g′(x)>0,g(x)單調遞增,
<x時,g′(x)>0,g(x)單調遞增,
所以![]()
![]() ,
,
令![]() ,則由
,則由![]() 得
得![]() ,
,
0<x<1時,t′(x)>0,t(x)單調遞增,1<x時,t′(x)<0,t(x)單調遞減,
所以![]() 在
在![]() 時取得極大值.
時取得極大值.
所以,當![]() ,
,![]() 的最小值
的最小值![]() ;
;
當![]() ,
,![]() 的最小值
的最小值![]() ,得
,得![]() ;
;
綜上,![]() .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,斜率為k的動直線l過點
中,斜率為k的動直線l過點![]() ,以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為
,以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)若直線l與曲線C有兩個交點,求這兩個交點的中點P的軌跡![]() 關于參數k的參數方程;
關于參數k的參數方程;
(2)在條件(1)下,求曲線![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x﹣a)cosx﹣sinx,g(x)![]() x3
x3![]() ax2,a∈R
ax2,a∈R
(1)當a=1時,求函數y=f(x)在區間(0,![]() )上零點的個數;
)上零點的個數;
(2)令F(x)=f(x)+g(x),試討論函數y=F(x)極值點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某市高三數學復習備考情況,該市教研機構組織了一次檢測考試,并隨機抽取了部分高三理科學生數學成績繪制如圖所示的頻率分布直方圖.
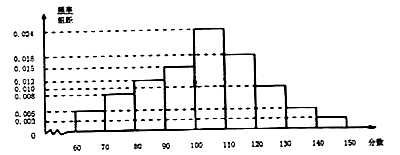
(1)根據頻率分布直方圖,估計該市此次檢測理科數學的平均成績![]() ;(精確到個位)
;(精確到個位)
(2)研究發現,本次檢測的理科數學成績![]() 近似服從正態分布
近似服從正態分布![]() (
(![]() ,
,![]() 約為
約為![]() ),按以往的統計數據,理科數學成績能達到自主招生分數要求的同學約占
),按以往的統計數據,理科數學成績能達到自主招生分數要求的同學約占![]() .
.
(ⅰ)估計本次檢測成績達到自主招生分數要求的理科數學成績大約是多少分?(精確到個位)
(ⅱ)從該市高三理科學生中隨機抽取![]() 人,記理科數學成績能達到自主招生分數要求的人數為
人,記理科數學成績能達到自主招生分數要求的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .(說明:
.(說明:![]() 表示
表示![]() 的概率.參考數據:
的概率.參考數據:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與x軸負半軸交于
與x軸負半軸交于![]() ,離心率
,離心率![]() .
.
(1)求橢圓C的方程;
(2)設直線![]() 與橢圓C交于
與橢圓C交于![]() 兩點,連接AM,AN并延長交直線x=4于
兩點,連接AM,AN并延長交直線x=4于![]() 兩點,若
兩點,若![]() ,直線MN是否恒過定點,如果是,請求出定點坐標,如果不是,請說明理由.
,直線MN是否恒過定點,如果是,請求出定點坐標,如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第十三屆全國人大常委會第十一次會議審議的《固體廢物污染環境防治法(修訂草案)》中,提出推行生活垃圾分類制度,這是生活垃圾分類首次被納入國家立法中.為了解某城市居民的垃圾分類意識與政府相關法規宣傳普及的關系,對某試點社區抽取![]() 戶居民進行調查,得到如下的
戶居民進行調查,得到如下的![]() 列聯表.
列聯表.
分類意識強 | 分類意識弱 | 合計 | |
試點后 |
| ||
試點前 |
| ||
合計 |
|
已知在抽取的![]() 戶居民中隨機抽取
戶居民中隨機抽取![]() 戶,抽到分類意識強的概率為
戶,抽到分類意識強的概率為![]() .
.
(1)請將上面的![]() 列聯表補充完整,并判斷是否有
列聯表補充完整,并判斷是否有![]() 的把握認為居民分類意識的強弱與政府宣傳普及工作有關?說明你的理由;
的把握認為居民分類意識的強弱與政府宣傳普及工作有關?說明你的理由;
(2)已知在試點前分類意識強的![]() 戶居民中,有
戶居民中,有![]() 戶自覺垃圾分類在
戶自覺垃圾分類在![]() 年以上,現在從試點前分類意識強的
年以上,現在從試點前分類意識強的![]() 戶居民中,隨機選出
戶居民中,隨機選出![]() 戶進行自覺垃圾分類年限的調查,記選出自覺垃圾分類年限在
戶進行自覺垃圾分類年限的調查,記選出自覺垃圾分類年限在![]() 年以上的戶數為
年以上的戶數為![]() ,求
,求![]() 分布列及數學期望.
分布列及數學期望.
參考公式: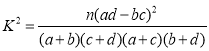 ,其中
,其中![]() .
.
下面的臨界值表僅供參考
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】詹姆斯·哈登(James Harden)是美國NBA當紅球星,自2012年10月加盟休斯頓火箭隊以來,逐漸成長為球隊的領袖.2017-18賽季哈登當選常規賽MVP(最有價值球員).
年份 | 2012-13 | 2013-14 | 2014-15 | 2015-16 | 2016-17 | 2017-18 |
年份代碼t | 1 | 2 | 3 | 4 | 5 | 6 |
常規賽場均得分y | 25.9 | 25.4 | 27.4 | 29.0 | 29.1 | 30.4 |
(Ⅰ)根據表中數據,求y關于t的線性回歸方程![]() (
(![]() ,
,![]()
![]() *);
*);
(Ⅱ)根據線性回歸方程預測哈登在2019-20賽季常規賽場均得分.
(附)對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:![]() ,
,![]()
(參考數據![]() ,計算結果保留小數點后一位)
,計算結果保留小數點后一位)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).以
為參數).以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ),將曲線
),將曲線![]() 向左平移2個單位長度得到曲線
向左平移2個單位長度得到曲線![]() .
.
(1)求曲線![]() 的普通方程和極坐標方程;
的普通方程和極坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有兩個調查抽樣:(1)某班為了了解班級學生在家表現情況決定從10名家長中抽取3名參加座談會;(2)某研究部門在高考后從2000名學生(其中文科400名,理科1600名)中抽取200名考生作為樣本調查數學學科得分情況.
給出三種抽樣方法:Ⅰ.簡單隨機抽樣法;Ⅱ.系統抽樣法;Ⅲ.分層抽樣法.
則問題(1)、(2)選擇的抽樣方法合理的是( )
A.(1)選Ⅲ,(2)選ⅠB.(1)選Ⅰ,(2)選Ⅲ
C.(1)選Ⅱ,(2)選ⅠD.(1)選Ⅲ,(2)選Ⅱ
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com