
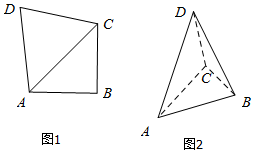
 如圖,在四邊形ABCD中,AB=BC=2,∠ABC=90°,DA=DC=$\sqrt{6}$.現(xiàn)沿對角線AC折起,使得平面DAC⊥平面ABC,此時點A,B,C,D在同一個球面上,則該球的體積是( )
如圖,在四邊形ABCD中,AB=BC=2,∠ABC=90°,DA=DC=$\sqrt{6}$.現(xiàn)沿對角線AC折起,使得平面DAC⊥平面ABC,此時點A,B,C,D在同一個球面上,則該球的體積是( )| A. | $\frac{9}{2}π$ | B. | $\frac{{8\sqrt{2}}}{3}π$ | C. | $\frac{27}{2}π$ | D. | 12π |
分析 根據(jù)兩平面的形狀尋找外球球的球心位置,利用勾股定理求出外接球半徑,從而可得出球的體積.
解答 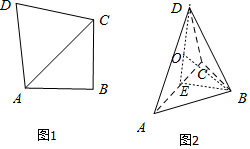 解:在圖2中,取AC的中點E,連結(jié)DE,BE,
解:在圖2中,取AC的中點E,連結(jié)DE,BE,
∵AD=CD,∴DE⊥AC,
∵平面ACD∩平面ABC=AC,平面ACD⊥平面ABC,
DE?平面ACD,
∴DE⊥平面ABC,
∵∠ABC=90°,
∴棱錐外接球的球心O在直線DE上,
∵AD=CD=$\sqrt{6}$,AB=BC=2,∠ABC=90°,
∴BE=AE=CE=$\frac{1}{2}$AC=$\sqrt{2}$,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=2,
設(shè)OE=x,則OD=2-x,OB=$\sqrt{B{E}^{2}+O{E}^{2}}$=$\sqrt{{x}^{2}+2}$,
∴2-x=$\sqrt{{x}^{2}+2}$,解得x=$\frac{1}{2}$,
∴外接球的半徑r=2-x=$\frac{3}{2}$,
∴外接球的體積V=$\frac{4π{r}^{3}}{3}$=$\frac{4π}{3}$×($\frac{3}{2}$)3=$\frac{9π}{2}$.
故選A.
點評 本題考查了棱錐與外接球的位置關(guān)系,球的體積計算,屬于中檔題.


科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 8π | B. | 16π | C. | 24π | D. | 32π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | S中沒有人認(rèn)識S中所有的人 | B. | S中至少有1人認(rèn)識S中所有的人 | ||
| C. | S中至多有2人不認(rèn)識S中所有的人 | D. | S中至多有2人認(rèn)識S中所有的人 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | arctan(-1)=$\frac{3π}{4}$ | B. | arctan($\frac{1}{2}$)=$\frac{π}{6}$ | C. | arcsin(-$\frac{1}{2}$)=-$\frac{π}{6}$ | D. | arccos(-$\frac{1}{2}$)=-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 1或2 | D. | 2或3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | (-1)n | D. | (-1)n-1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com