
分析 方法一:設直線的斜率,代入橢圓方程,根據韋達定理及中點坐標公式,即可求得直線的斜率,求得直線方程;
方法二:設弦的兩端點坐標為(x1,y1)、(x2,y2),代入橢圓方程,作差,即可求得直線的斜率,求得的直線方程;
方法三:設過P的弦與橢圓相交于M(1+m,1+n),N(1-m,1-n),代入橢圓方程,作差,即可求得m+2n=0,則直線k=$\frac{n}{m}$=-$\frac{1}{2}$,求得的直線方程;
解答 解:解法一:易知引弦所在直線的斜率存在,則設其方程為y-1=k(x-1),
弦的兩端點為(x1,y1),(x2,y2).
由$\left\{\begin{array}{l}{y-1=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去y得(2k2+1)x2-4k(k-1)x+2(k2-2k-1)=0,
∴x1+x2=$\frac{4k(k-1)}{2{k}^{2}+1}$.
又∵x1+x2=2,∴$\frac{4k(k-1)}{2{k}^{2}+1}$=2,得k=-$\frac{1}{2}$.
故弦所在直線方程為y-1=-$\frac{1}{2}$(x-1),即x+2y-3=0.
解法二:由于此弦所在直線的斜率存在,所以設斜率為k,且設弦的兩端點坐標為(x1,y1)、(x2,y2),
則$\frac{{x}_{1}^{2}}{4}$+$\frac{{y}_{1}^{2}}{2}$=1,$\frac{{x}_{2}^{2}}{4}$+$\frac{{y}_{2}^{2}}{2}$=1,兩式相減得
$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{4}$+$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{2}$=0.
∵x1+x2=2,y1+y2=2,
∴$\frac{x1-x2}{2}$+(y1-y2)=0,
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{1}{2}$.
∴此弦所在直線方程為y-1=-$\frac{1}{2}$(x-1),即x+2y-3=0.
∴此弦所在的直線方程x+2y-3=0.
方法三:由題意可知:過P的弦與橢圓相交于M(1+m,1+n),N(1-m,1-n),
由M,N在橢圓方程:$\frac{(1+m)^{2}}{4}+\frac{(1+n)^{2}}{2}=1$,$\frac{(1-m)^{2}}{4}+\frac{(1-n)^{2}}{2}=1$,
兩式相減得:m+2n=0,
則直線MN的斜率k=$\frac{(1+n)-(1-n)}{(1+m)-(1-m)}$=$\frac{n}{m}$=-$\frac{1}{2}$,
此弦所在直線方程為y-1=-$\frac{1}{2}$(x-1),即x+2y-3=0.
點評 本題考查直線與橢圓的位置關系,考查直線的點斜式方程,點差法的應用,方法多,注意靈活應用,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
| 月份x | 1 | 2 | 3 | 4 | 5 |
| y(萬盒) | 4 | 4 | 5 | 6 | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
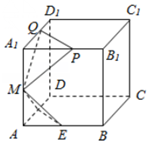 已知棱長為l的正方體ABCD-A1B1C1D1中,E,F,M分別是AB、AD、AA1的中點,又P、Q分別在線段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,設面MEF∩面MPQ=l,則下列結論中不成立的是( )
已知棱長為l的正方體ABCD-A1B1C1D1中,E,F,M分別是AB、AD、AA1的中點,又P、Q分別在線段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,設面MEF∩面MPQ=l,則下列結論中不成立的是( )| A. | l∥面ABCD | B. | l⊥AC | ||
| C. | 面MEF與面MPQ垂直 | D. | 當x變化時,l是定直線 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在海岸A處,發現北偏東45°方向,距離A為$(\sqrt{3}-1)$海里的B處有一艘走私船,在A處北偏西75°方向,距離A為2 海里的C處有一艘緝私艇奉命以$10\sqrt{3}$海里/時的速度追截走私船,此時,走私船正以10 海里/時的速度從B處向北偏東30°方向逃竄
在海岸A處,發現北偏東45°方向,距離A為$(\sqrt{3}-1)$海里的B處有一艘走私船,在A處北偏西75°方向,距離A為2 海里的C處有一艘緝私艇奉命以$10\sqrt{3}$海里/時的速度追截走私船,此時,走私船正以10 海里/時的速度從B處向北偏東30°方向逃竄查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com