
分析 (1)根據偶函數可知f(x)=f(-x),取x=-1代入即可求出k的值;
(2)由(1)中結論,可以得到函數的解析式,構造函數y=log4(4x+1)-x,分析出函數的單調性及值域,根據函數零點的判定方法,我們易確定b取不同值時,函數零點個數,進而得到答案.
(3)問題轉化為y=t2+mt在t∈[1,3]上最小值為0,分類討論,即可求出m的值.
解答 解:(1)∵f(x)=log4(4x+1)+kx(k∈R)的圖象關于y軸對稱.
∴函數f(x)是偶函數.
∴f(-x)=f(x)
即log4(4-x+1)-kx=log4(4x+1)+kx
即log4(4x+1)-(k+1)x=log4(4x+1)+kx
即2k+1=0
∴k=-$\frac{1}{2}$;
證明:(2)由(1)得f(x)=log4(4x+1)=-$\frac{1}{2}$x,
令y=log4(4x+1)-x-a
由于y=log4(4x+1)-x-a為減函數,且恒為正,
故當a>0時,y=log4(4x+1)-x-a有唯一的零點,
此時函數y=f(x)的圖象與直線y=$\frac{1}{2}$x+a有一個交點,
當a≤0時,y=log4(4x+1)-x-a沒有零點,
此時函數y=f(x)的圖象與直線y=$\frac{1}{2}$x+a沒有交點,
綜上所述,a≤0時,函數y=f(x)的圖象與直線y=$\frac{1}{2}$x+a沒有交點;
(3)h(x)=4${\;}^{f(x)+\frac{1}{2}x}$+m•2x-1=4x+m-2x,x∈[0,log23]
設t=2x,則t∈[1,3]
∴y=t2+mt在t∈[1,3]上最小值為0
又∵y=(t+$\frac{m}{2}$)2-$\frac{{m}^{2}}{4}$,t∈[1,3],
當-$\frac{m}{2}$≤1 即m≥-2時,t=1時ymin=m+1=0,
∴m=-1,符合,
當-1<-$\frac{m}{2}$<3 即-6<m<-2時,t=-$\frac{m}{2}$時,ymin=-$\frac{{m}^{2}}{4}$=0
∴m=0 不符合
當-$\frac{m}{2}$≥3 即m≤-6時,t=3時,ymin=9+3m=0,
∴m=-3,符合,
綜上所述m的值為-3,-1.
點評 本題主要考查了偶函數的性質,以及對數函數圖象與性質的綜合應用,同時考查了分類討論的思想,由于綜合考查了多個函數的難點,屬于難題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
 已知關于x的二次函數f(x)=ax2-4bx+1.
已知關于x的二次函數f(x)=ax2-4bx+1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
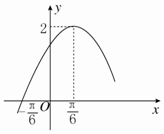 函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分圖象如圖所示.
函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com