
| A. | (-2,-1) | B. | (-1,+∞) | C. | (-1,2) | D. | (2,+∞) |
分析 設g(x)=f(x+1)-ln(x+2)-2-ex+1-3x,x>-2,求導g′(x)=f′(x+1)-$\frac{1}{x+2}$-ex+1-3,由f′(x)<2,f′(x+1)-3<0,由-$\frac{1}{x+2}$-ex+1<0恒成立,因此g′(x)<0恒成立,則g(x)在(-2,+∞)單調遞減,根據函數的奇偶性可知f(0)=0,可得g(-1)=0,則原不等式可轉化成,g(x)=g(-1),由函數的單調性即可求得-2<x<-1.
解答 解:由題意可知:設g(x)=f(x+1)-ln(x+2)-2-ex+1-3x,x>-2,
求導g′(x)=f′(x+1)-$\frac{1}{x+2}$-ex+1-3,
由f′(x)<2,即f′(x)-2<0,
f′(x+1)-3<0,
由函數的單調性可知:-$\frac{1}{x+2}$-ex+1<0恒成立,
∴g′(x)<0恒成立,
∴g(x)在(-2,+∞)單調遞減,
由y=f(x)為奇函數,則f(0)=0
∴g(-1)=f(0)-ln1-2-e0+3=0,
由f(x+1)-ln(x+2)-2>ex+1+3x,即g(x)>0=g(-1),
由函數的單調遞減,
∴-2<x<-1,
∴不等式f(x+1)-ln(x+2)-2>ex+1+3x的解集(-2,-1),
故選A.
點評 本題考查函數的單調性與導數的關系,考查利用導數求函數的單調性,考查不等式的解集的求法,考查轉化思想,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | M∩N={ 4,6 } | B. | M∪N=U | C. | (∁UN )∪M=U | D. | (∁UM)∩N=N |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
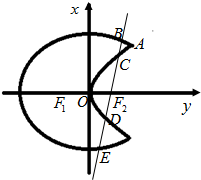 如圖,曲線C1是橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其兩焦點.曲線C2是以原點O為頂點、F2為焦點的拋物線的一部分,A是曲線C1和C2的一個公共點,并且∠AF2F1為鈍角.我們把由曲線C1和C2合成的曲線C稱為“月食圓”.
如圖,曲線C1是橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其兩焦點.曲線C2是以原點O為頂點、F2為焦點的拋物線的一部分,A是曲線C1和C2的一個公共點,并且∠AF2F1為鈍角.我們把由曲線C1和C2合成的曲線C稱為“月食圓”.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x>0,cosx+sinx>1 | B. | ?x0≤0,cosx0+sinx0≤1 | ||
| C. | ?x>0,cosx+sinx≤1 | D. | ?x0>0,cosx0+sinx0≤1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G為線段PC上的點,
如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G為線段PC上的點,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
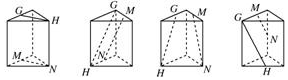
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com