
已知函數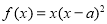 ,
,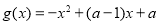 (其中
(其中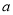 為常數).
為常數).
(1)如果函數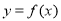 和
和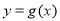 有相同的極值點,求
有相同的極值點,求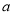 的值;
的值;
(2)設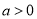 ,問是否存在
,問是否存在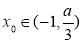 ,使得
,使得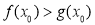 ,若存在,請求出實數
,若存在,請求出實數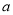 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
(3)記函數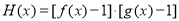 ,若函數
,若函數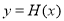 有5個不同的零點,求實數
有5個不同的零點,求實數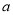 的取值范圍.
的取值范圍.
(1)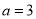 或
或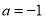 ;(2)
;(2)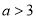 ;(3)
;(3)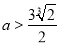 .
.
【解析】
試題分析:本題主要考查導數的運算、利用導數求函數的極值和最值、利用導數判斷函數的單調性、求函數的零點等基礎知識,考查學生的分析問題解決問題的能力、轉化能力、計算能力.第一問,對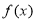 求導,得到
求導,得到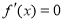 有2個根,而
有2個根,而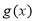 在
在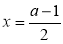 處有極大值,所以那2個根分別等于
處有極大值,所以那2個根分別等于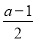 ,得到a的值;第二問,假設存在
,得到a的值;第二問,假設存在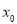 使得
使得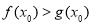 ,將
,將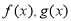 代入得到解析式,由于
代入得到解析式,由于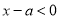 ,所以將問題轉化成了存在
,所以將問題轉化成了存在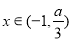 ,使得
,使得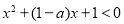 ,分類討論,討論拋物線的對稱軸和區間端點的大小,數形結合,得到結論;第三問,已知條件中
,分類討論,討論拋物線的對稱軸和區間端點的大小,數形結合,得到結論;第三問,已知條件中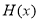 有5個不同的零點,根據
有5個不同的零點,根據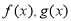 解析式的特點,知
解析式的特點,知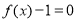 有3個不同的實根,
有3個不同的實根,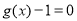 有2個不同的實根,通過拋物線的圖形可知要使
有2個不同的實根,通過拋物線的圖形可知要使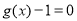 有2個不同的實根,只需
有2個不同的實根,只需 ,而
,而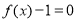 ,通過第一問得到的極值點,討論2個數的3種大小關系,結合圖象,確定a的取值范圍,a的取值范圍需保證
,通過第一問得到的極值點,討論2個數的3種大小關系,結合圖象,確定a的取值范圍,a的取值范圍需保證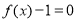 和
和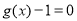 同時成立,還得保證這5個根互不相等.
同時成立,還得保證這5個根互不相等.
試題解析:(1)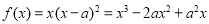 ,則
,則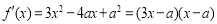 ,
,
令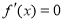 ,得
,得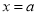 或
或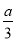 ,而
,而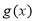 在
在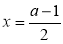 處有極大值,
處有極大值,
∴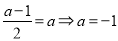 或
或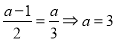 ;綜上:
;綜上: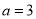 或
或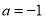 . 3分
. 3分
(2)假設存在,即存在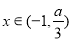 ,使得
,使得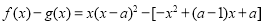
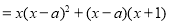
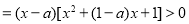 ,
,
當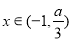 時,又
時,又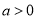 ,故
,故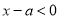 ,則存在
,則存在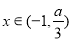 ,使得
,使得
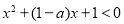 , 4分
, 4分
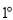 當
當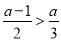 即
即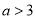 時,
時,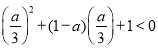 得
得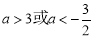 ,
,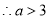 ;
;
5分
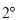 當
當 即
即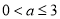 時,
時,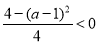 得
得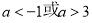 , 6分
, 6分
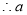 無解;綜上:
無解;綜上: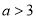 . 7分
. 7分
(3)據題意有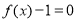 有3個不同的實根,
有3個不同的實根,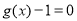 有2個不同的實根,且這5個實根兩兩不相等.\(ⅰ)
有2個不同的實根,且這5個實根兩兩不相等.\(ⅰ)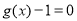 有2個不同的實根,只需滿足
有2個不同的實根,只需滿足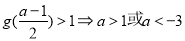 ; 8分
; 8分
(ⅱ)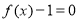 有3個不同的實根,
有3個不同的實根,
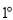 當
當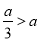 即
即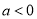 時,
時,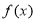 在
在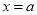 處取得極大值,而
處取得極大值,而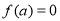 ,不符合題意,舍; 9分
,不符合題意,舍; 9分
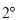 當
當 即
即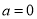 時,不符合題意,舍;
時,不符合題意,舍;
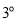 當
當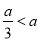 即
即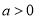 時,
時,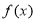 在
在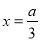 處取得極大值,
處取得極大值,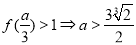 ;所以
;所以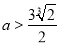 ; 10分
; 10分
因為(ⅰ)(ⅱ)要同時滿足,故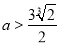 ;(注:
;(注: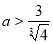 也對) 11分
也對) 11分
下證:這5個實根兩兩不相等,即證:不存在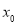 使得
使得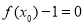 和
和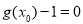 同時成立.
同時成立.
若存在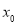 使得
使得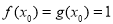 ,
,
由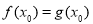 ,即
,即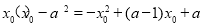 ,得
,得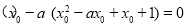 ,
,
當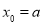 時,
時,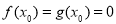 ,不符合,舍去;
,不符合,舍去;
當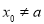 時,既有
時,既有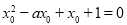 ①;
①;
又由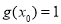 ,即
,即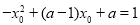 ②; 聯立①②式,可得
②; 聯立①②式,可得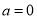 ;
;
而當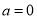 時,
時,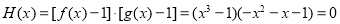 沒有5個不
沒有5個不
同的零點,故舍去,所以這5個實根兩兩不相等.
綜上,當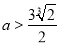 時,函數
時,函數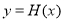 有5個不同的零點. 14分
有5個不同的零點. 14分
考點:導數的運算、利用導數求函數的極值和最值、利用導數判斷函數的單調性、求函數的零點.


 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:高中數學 來源:2013-2014學年廣東省廣州市畢業班綜合測試二文科數學試卷(解析版) 題型:選擇題
設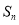 是等差數列
是等差數列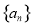 的前
的前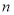 項和,公差
項和,公差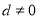 ,若
,若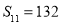 ,若
,若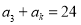 ,則正整數
,則正整數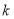 的值為( )
的值為( )
A.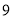 B.
B.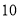 C.
C.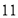 D.
D.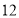
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三第二次模擬考試文科數學試卷(解析版) 題型:選擇題
已知雙曲線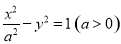 的右焦點與拋物線
的右焦點與拋物線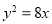 焦點重合,則此雙曲線的漸近線方程是( )
焦點重合,則此雙曲線的漸近線方程是( )
A.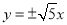 B.
B.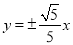
C.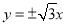 D.
D.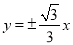
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三模擬(一)理科數學試卷(解析版) 題型:填空題
已知集合A={x|x2-2x-3>0 },B={x|ax2+bx+c≤0},若A∩B={x|3<x≤4},
A∪B=R,則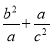 的最小值為____.
的最小值為____.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三模擬(一)理科數學試卷(解析版) 題型:選擇題
給出下列三個結論:
(1)若命題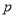 為假命題,命題
為假命題,命題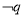 為假命題,則命題“
為假命題,則命題“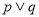 ”為假命題;
”為假命題;
(2)命題“若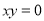 ,則
,則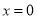 或
或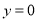 ”的否命題為“若
”的否命題為“若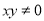 ,則
,則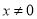 或
或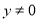 ”;
”;
(3)命題“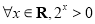 ”的否定是“
”的否定是“ 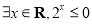 ”.則以上結論正確的個數為( )
”.則以上結論正確的個數為( )
A.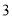 B.
B.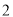 C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三模擬(一)文科數學試卷(解析版) 題型:解答題
設函數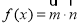 ,其中向量
,其中向量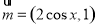 ,
,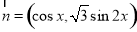 ,
,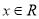 .
.
(1)求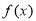 的單調遞增區間;
的單調遞增區間;
(2)在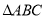 中,
中,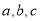 分別是角
分別是角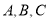 的對邊,已知
的對邊,已知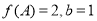 ,
,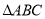 的面積為
的面積為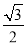 ,求
,求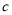 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三模擬(一)文科數學試卷(解析版) 題型:選擇題
已知 ,
,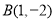 ,
,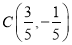 ,動點
,動點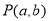 滿足
滿足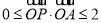 且
且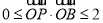 ,則點
,則點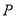 到點
到點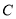 的距離大于
的距離大于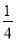 的概率為( )
的概率為( )
A.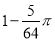 B.
B.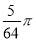 C.
C. D.
D.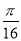
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com