
分析 (1)利用三角函數間的恒等變換可求得f(x)=2sin(2x+$\frac{π}{3}$),利用函數y=Asin(ωx+φ)的圖象變換可求得g(x)=2sinx;
(2)根據余弦定理和正弦函數的性質即可求出.
解答 解:(1)$\overrightarrow{m}$=(1,cos2x),$\overrightarrow{n}$=(sin2x,$\sqrt{3}$),
函數f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=sin2x+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),
∵將函數y=f(x)的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),
再將所得圖象向右平移$\frac{π}{3}$個單位,所得函數圖象對應的解析式記為g(x).
∴g(x)=2sinx,
(2)∵a2+c2-b2=ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$,
∴B=$\frac{π}{3}$,
∵A+B+C=π,
∴A=$\frac{2π}{3}$-C,
∴0<A<$\frac{2π}{3}$,
∴$\frac{π}{3}$<2A+$\frac{π}{3}$<$\frac{5}{3}$π,
∴f(A)=2sin(2A+$\frac{π}{3}$),
∴當2A+$\frac{π}{3}$=$\frac{π}{2}$時,有最大值,最大值為2,
當2A+$\frac{π}{3}$=$\frac{3π}{2}$時,有最小值,最小值為-2.
∴-2≤f(A)≤2.
點評 本題考查二倍角的余弦,考查三角函數間的恒等變換,突出考查函數y=Asin(ωx+φ)的圖象變換及與余弦定理,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | 16 | B. | 20 | C. | 24 | D. | 18 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①③④ | B. | ②④⑤ | C. | ③④⑤ | D. | ②③⑤ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
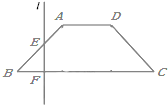 如圖,已知底角為45°的等腰梯形ABCD,底邊BC長為7cm,腰長為2$\sqrt{2}$cm,當一條垂直于底邊BC(垂足為F)的直線l從左至右移動(與梯形ABCD有公共點)時,直線l把梯形分成兩部分,令BF=x,
如圖,已知底角為45°的等腰梯形ABCD,底邊BC長為7cm,腰長為2$\sqrt{2}$cm,當一條垂直于底邊BC(垂足為F)的直線l從左至右移動(與梯形ABCD有公共點)時,直線l把梯形分成兩部分,令BF=x,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {7,9} | B. | {0,3,7,9,4,5} | C. | {5,7,9} | D. | ∅ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com