
分析 根據二倍角公式可知-$\frac{1}{2}≤$sinαcosα≤$\frac{1}{2}$,故①錯誤;根據誘導公式,可知sin($\frac{3}{2}π$+x)=-cosx,故②正確;x=$\frac{π}{8}$時,y=sin$\frac{3}{2}π$=-1,故③正確;α=390°,β=60°時,sinα<sinβ,故④錯誤;利用誘導公式化簡,y=2sin($\frac{π}{3}$-x)-cos($\frac{π}{6}$+x)=cos($\frac{π}{6}$+x),故⑤正確;函數周期為$\frac{π}{2}$,故⑥錯誤.
解答 解:對于①:∵sinαcosα=$\frac{1}{2}×2sinαcosα=\frac{1}{2}sin2α$,∴$-\frac{1}{2}≤sinαcosα≤\frac{1}{2}$,故①錯誤;
對于②:∵y=sin($\frac{3}{2}π$+x)=sin[$π+(\frac{π}{2}+x)$]=-sin($\frac{π}{2}+x$)=-cosx,且-cos(-x)=-cosx,∴$y=sin(\frac{3}{2}π+x)$是偶函數,故②正確;
對于③:當x=$\frac{π}{8}$時,y=sin$\frac{3}{2}π$=-1,所以直線$x=\frac{π}{8}$是函數$y=sin(2x+\frac{5}{4}π)$的一條對稱軸,故③正確;
對于④:舉反例,例如α=390°,β=60°時,sin390°=$\frac{1}{2}$,sin60°=$\frac{\sqrt{3}}{2}$,即sinα<sinβ,故④錯誤;
對于⑤:∵y=2sin($\frac{π}{3}$-x)-cos($\frac{π}{6}+x)$=2sin[$\frac{π}{2}-(x+\frac{π}{6})$]-cos(x+$\frac{π}{6}$)=2cos(x+$\frac{π}{6}$)-cos(x+$\frac{π}{6}$)=cos(x+$\frac{π}{6}$),∴ymin=-1,故⑤正確;
對于⑥:由圖象可知,y=|tan(2x+$\frac{π}{3}$)|與y=tan(2x+$\frac{π}{3}$)的周期相同,T=$\frac{π}{2}$,故⑥錯誤.
故答案為:②③⑤
點評 本題通過命題的真假判斷考查了誘導公式,三角函數的圖象和性質以及三角恒等變換,屬于中檔題.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-6)∪(6,+∞) | B. | (-∞,-4)∪(4,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
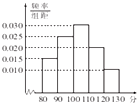 某班k名學生在一次考試中數學成績繪制的頻率分布直方圖如圖,若在這k名學生中,數學成績不低于90分的人數為34,則k=( )
某班k名學生在一次考試中數學成績繪制的頻率分布直方圖如圖,若在這k名學生中,數學成績不低于90分的人數為34,則k=( )| A. | 40 | B. | 46 | C. | 48 | D. | 50 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com