
 如圖所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是側面ABB'A'的中心,點D、E、F分別是棱A'C'、AB、BB'的中點.
如圖所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是側面ABB'A'的中心,點D、E、F分別是棱A'C'、AB、BB'的中點.分析 (1)側面AA′B′B為正方形,連結A′B,則O為A′B的中點,從而OD∥BC′,由此能證明OD∥平面BCC'B'.
(2)取BC中點M,連結EM、FM,則∠FEM為異面直線EF與AC所成的角,由此能求出直線EF和AC所成的角.
解答 證明:(1)依題意可知側面AA′B′B為正方形,連結A′B,則O為A′B的中點,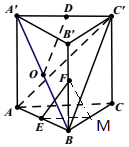 在△A′BC′中,O、D分別是邊A′B、A′C′的中點,
在△A′BC′中,O、D分別是邊A′B、A′C′的中點,
∴OD∥BC′,
∵BC′?平面BCC'B',OD?平面BCC'B',
∴OD∥平面BCC'B'.
解:(2)取BC中點M,連結EM、FM,
則∠FEM為異面直線EF與AC所成的角,
設AB=2,則EM=EF=FM=$\sqrt{2}$,∴∠FEM=60°,
∴直線EF和AC所成的角為60°.
點評 本題考查線面平行的證明,考查異面直線所成角的求法,考查空間中線線、線面、面面間的位置關系,考查推理論證能力、運算求解能力,是中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
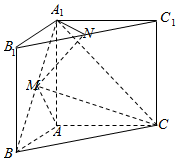 在三棱柱ABC-A1B1C1中,側棱與底面垂直,AB=AA1=2,∠ABC=60°,BC=4,點M,N分別為A1B 和B1C1的中點.
在三棱柱ABC-A1B1C1中,側棱與底面垂直,AB=AA1=2,∠ABC=60°,BC=4,點M,N分別為A1B 和B1C1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{10}}}{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com