
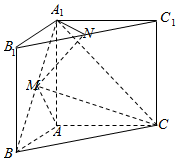
 在三棱柱ABC-A1B1C1中,側(cè)棱與底面垂直,AB=AA1=2,∠ABC=60°,BC=4,點(diǎn)M,N分別為A1B 和B1C1的中點(diǎn).
在三棱柱ABC-A1B1C1中,側(cè)棱與底面垂直,AB=AA1=2,∠ABC=60°,BC=4,點(diǎn)M,N分別為A1B 和B1C1的中點(diǎn).分析 (1)取A1B1的中點(diǎn)D,連結(jié)MD、ND,推導(dǎo)出DM∥AA1,DN∥A1C1,從而平面DMN∥平面A1ACC1,由此能證明MN∥平面A1ACC1.
(2)推導(dǎo)出AM⊥A1B,由余弦定理得AC=2$\sqrt{3}$,從而${A}_{1}C=\sqrt{A{{A}_{1}}^{2}+A{C}^{2}}$=4,進(jìn)而CM⊥A1B,由此能證明A1M⊥平面MAC.
解答 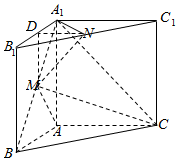 證明:(1)取A1B1的中點(diǎn)D,連結(jié)MD、ND,
證明:(1)取A1B1的中點(diǎn)D,連結(jié)MD、ND,
∵在三棱柱ABC-A1B1C1中,側(cè)棱與底面垂直,點(diǎn)M,N分別為A1B 和B1C1的中點(diǎn),
∴DM∥AA1,DN∥A1C1,
∵DM∩DN=D,AA1∩A1C1=A1,
DM,DN?平面DMN,AA1,A1C1?平面A1ACC1,
∴平面DMN∥平面A1ACC1,
∵M(jìn)N?平面DMN,∴MN∥平面A1ACC1.
(2)∵側(cè)棱與底面垂直,AB=AA1=2,∠ABC=60°,BC=4,
點(diǎn)M,N分別為A1B 和B1C1的中點(diǎn),
∴AM⊥A1B,AC=$\sqrt{{2}^{2}+{4}^{2}-2×2×4×cos60°}$=2$\sqrt{3}$,
${A}_{1}C=\sqrt{A{{A}_{1}}^{2}+A{C}^{2}}$=$\sqrt{4+12}$=4,∴CM⊥A1B,
∵AM∩CM=M,∴A1M⊥平面MAC.
點(diǎn)評(píng) 本題考查線面平行的證明,考查線面垂直的證明,考查空間中線線、線面、面面間的位置關(guān)系等基礎(chǔ)知識(shí),考查推理論證能力、運(yùn)算求解能力,考查化歸與轉(zhuǎn)化思想,是中檔題.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | 2a>2b | C. | |a|>|b| | D. | a2>b2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
| ωx+$\frac{π}{6}$ | |||||
| x | |||||
| f(x) |

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是側(cè)面ABB'A'的中心,點(diǎn)D、E、F分別是棱A'C'、AB、BB'的中點(diǎn).
如圖所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是側(cè)面ABB'A'的中心,點(diǎn)D、E、F分別是棱A'C'、AB、BB'的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com