
分析 (1)代值計(jì)算即可,并猜想一般的結(jié)論,
(2)由(1)$f(x)+f({\frac{1}{x}})=1$,即可得出結(jié)論.
解答 解:(1)∵$f(x)=\frac{x^2}{{1+{x^2}}}$,
∴$f(2)+f({\frac{1}{2}})=\frac{2^2}{{1+{2^2}}}+\frac{{{{({\frac{1}{2}})}^2}}}{{1+{{({\frac{1}{2}})}^2}}}=\frac{2^2}{{1+{2^2}}}+\frac{1}{{1+{2^2}}}=1$,
同理可得$f(3)+f({\frac{1}{3}})=1,f(4)+f({\frac{1}{4}})=1$,
猜想$f(x)+f({\frac{1}{x}})=1$.
(2)∵$f(x)+\frac{1}{x^2}f(x)=\frac{x^2}{{1+{x^2}}}({1+\frac{1}{x^2}})=1$,
又由(1)得,$f(x)+f({\frac{1}{x}})=1$,
則$2f(2)+2f(3)+…2f({2017})+f({\frac{1}{2}})+f({\frac{1}{3}})+…f({\frac{1}{2017}})+\frac{1}{2^2}f(2)+\frac{1}{3^2}f(3)+…\frac{1}{{{{2017}^2}}}f({2017})$
=$[{f(2)+f({\frac{1}{2}})+f(2)+\frac{1}{2^2}f({\frac{1}{2}})}]+[{f(3)+f({\frac{1}{3}})+f(3)+\frac{1}{3^2}f({\frac{1}{3}})}]+$$…[{f({2017})+f({\frac{1}{2017}})+f({2017})+\frac{1}{{{{2017}^2}}}f({\frac{1}{2017}})}]=2×2016=4032$.
點(diǎn)評(píng) 本題考查歸納推理,考查學(xué)生的計(jì)算能力,正確歸納是關(guān)鍵,屬于中檔題



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 1+2i | B. | 1-2i | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
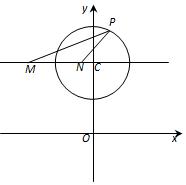 已知圓C:x2+(y-4)2=4,直線l:(3m+1)x+(1-m)y-4=0
已知圓C:x2+(y-4)2=4,直線l:(3m+1)x+(1-m)y-4=0查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| 男 | 女 | 總計(jì) | |
| 愛好 | 10 | 40 | 50 |
| 不愛好 | 20 | 30 | 50 |
| 總計(jì) | 30 | 70 | n |
| A. | 1% | B. | 2.5% | C. | 5% | D. | 10% |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
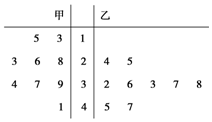 如圖是某賽季甲、乙兩名籃球運(yùn)動(dòng)員每場(chǎng)比賽得分的莖葉圖,甲、乙兩人這幾場(chǎng)比賽得分的平均數(shù)分別為$\overline{x_甲}$,$\overline{x_乙}$;準(zhǔn)差分別是s甲,s乙,則有( )
如圖是某賽季甲、乙兩名籃球運(yùn)動(dòng)員每場(chǎng)比賽得分的莖葉圖,甲、乙兩人這幾場(chǎng)比賽得分的平均數(shù)分別為$\overline{x_甲}$,$\overline{x_乙}$;準(zhǔn)差分別是s甲,s乙,則有( )| A. | $\overline{x_甲}$<$\overline{x_乙}$,s甲<s乙 | B. | $\overline{x_甲}$<$\overline{x_乙}$,s甲>s乙 | ||
| C. | $\overline{x_甲}$>$\overline{x_乙}$,s甲<s乙 | D. | $\overline{x_甲}$>$\overline{x_乙}$,s甲>s乙 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com