
分析 分別求出$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…,$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+$\frac{1}{{3}^{4}}$+…,$\frac{1}{{(n+)}^{2}}$+$\frac{1}{{(n+1)}^{3}}$+$\frac{1}{{(n+1)}^{4}}$+…的極限,再代入∑n-1φ∑m-1φ$\frac{1}{{(n+1)}^{m+1}}$中,通過裂項法求得答案.
解答 解:$\sum_{n=1}^∞{\sum_{m=1}^∞{\frac{1}{{{{(n+1)}^{m+1}}}}}}$=$(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+…)+(\frac{1}{3^2}+\frac{1}{3^3}+\frac{1}{3^4}+…)+…+(\frac{1}{{{{(n+1)}^2}}}+\frac{1}{{{{(n+1)}^3}}}+\frac{1}{{{{(n+1)}^4}}}+…)+…$
=$\frac{\frac{1}{{2}^{2}}}{1-\frac{1}{2}}$+$\frac{\frac{1}{{3}^{2}}}{1-\frac{1}{3}}$+…+$\frac{\frac{1}{{(n+1)}^{2}}}{1-\frac{1}{n+1}}$
=$\frac{1}{2}$+$\frac{1}{2}$×$\frac{1}{3}$+$\frac{1}{3}$×$\frac{1}{4}$+…+$\frac{1}{n}$×$\frac{1}{n+1}$
=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)
=1-$\frac{1}{n+1}$,
當n→+∞時,$\sum_{n=1}^∞{\sum_{m=1}^∞{\frac{1}{{{{(n+1)}^{m+1}}}}}}$=1.
故答案為:$\sum_{n=1}^∞{\sum_{m=1}^∞{\frac{1}{{{{(n+1)}^{m+1}}}}}}$=1.
點評 本題主要考查了用裂項法求和的應用問題,是綜合性問題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | -7 | B. | -8 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 空間中過直線外一點有且僅有一條直線與該直線垂直 | |
| B. | 僅存在一個實數b2,使得-9,b1,b2,b3,-1成等比數列 | |
| C. | 存在實數a,b滿足a+b=2,使得3a+3b的最小值是6 | |
| D. | ?a∈(-4,0],ax2+ax-1<0恒成立 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
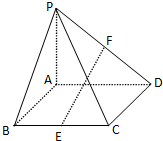 如圖,在四棱錐P-ABCD中,底面ABCD為矩形,側棱PA⊥底面ABCD,點E,F分別為BC、PD的中點,若PA=AD=4,AB=2.
如圖,在四棱錐P-ABCD中,底面ABCD為矩形,側棱PA⊥底面ABCD,點E,F分別為BC、PD的中點,若PA=AD=4,AB=2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com