
分析 (Ⅰ)運用離心率公式和最大值a+c,解方程即可得到a,c,求出b,進而得到橢圓方程;
(Ⅱ)求出A,B坐標,考慮MN斜率不存在,可得M,N坐標,求出直線AN,BN方程,求出交點,猜想:存在l:x=-8,再由分析法證明,設MN的方程是y=k(x+2),代入橢圓C的方程,運用韋達定理,即可得到存在定直線l:x=-8,使得AM與BN的交點Q總在直線l上.
解答 解:(Ⅰ)由$e=\frac{{\sqrt{3}}}{2}⇒\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,
又橢圓C上的點到焦點的距離的最大值$a+c=4+2\sqrt{3}$.
∴a=4,c=2$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{16-12}$=2,
所以橢圓C方程是:$\frac{x^2}{16}+\frac{y^2}{4}=1$;
(Ⅱ)證明:A(-4,0).B(4,0),
當MN斜率不存在時,MN:x=-2,$M(-2,\sqrt{3}),N(-2,-\sqrt{3})$,
則AN的方程是:y=$\frac{\sqrt{3}}{2}$(x+4),
BN的方程是:y=$\frac{\sqrt{3}}{6}$(x-4),
交點的坐標是:$(-8,-2\sqrt{3})$,猜想:存在l:x=-8,
即直線l的方程是:x=-8使得AM與BN的交點Q總在直線l上.
當MN斜率存在時,設MN的方程是y=k(x+2),代入橢圓C的方程得:
(1+4k2)x2+16k2x+16k2-16=0,
設M(x1,y1),N(x2,y2),Q(-8,y0)
∴${x_1}+{x_2}=\frac{{-16{k^2}}}{{1+4{k^2}}},{x_1}{x_2}=\frac{{16{k^2}-16}}{{1+4{k^2}}}$,
∵$\overrightarrow{AQ}=(-4,{y_0})$,$\overrightarrow{AM}$=(x1+4,y1),A,M,Q共線,
∴-4y1=y0(x1+4),
由x1+4≠0,可得y0=-$\frac{4{y}_{1}}{{x}_{1}+4}$,
又$\overrightarrow{BQ}=(-12,{y_0})$,$\overrightarrow{BN}=({x_2}-4,{y_2})$,
要證B,N,Q共線,即證$-12{y_2}=({x_2}-4)\frac{{-4{y_1}}}{{{x_1}+4}}$,
即證:3k(x2+2)(x1+4)=k(x1+2)(x2-4),
即證:x1x2+5(x1+x2)+16=0
因為:${x_1}{x_2}+5({x_1}+{x_2})+16=\frac{{16{k^2}-16}}{{1+4{k^2}}}-\frac{{80{k^2}}}{{1+4{k^2}}}+16=0$成立,
所以點Q在直線BN上.
綜上:AM與BN的交點Q總在定直線l:x=-8上.
點評 本題考查橢圓方程求法,注意運用離心率公式和橢圓上點與焦點的最大值a+c,考查定直線問題的證明,注意運用猜想和分析法,考查化簡整理的運算能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,0)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪(0,1) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{7}$ | B. | $\frac{7}{10}$ | C. | $\frac{24}{35}$ | D. | $\frac{47}{70}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
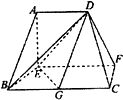 在如圖所示的多面體中,底面BCFE是梯形,EF∥BC,EF⊥EB,又平面ABE⊥平面BCFE,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$.
在如圖所示的多面體中,底面BCFE是梯形,EF∥BC,EF⊥EB,又平面ABE⊥平面BCFE,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
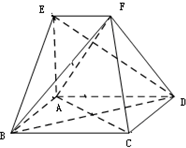 在如圖所示的幾何體中,四邊形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.
在如圖所示的幾何體中,四邊形ABCD是正方形,EA⊥底面ABCD,EF∥AD,且AB=6,AE=3$\sqrt{2}$,EF=3.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com