
分析 (1)化簡f(x)的解析式,求出函數的對稱軸即可;
(2)降冪后利用兩角差的正弦函數化積,然后利用x的取值范圍求得函數的最大值和最小值;
(3)不等式|f(x)-m|<2在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上恒成立,轉化為m-2<f(x)<m+2在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上恒成立,進一步轉化為m-2,m+2與函數f(x)在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上的最值的關系,列不等式后求得實數m的取值范圍.
解答 解:(1)f(x)=2cos2(x-$\frac{π}{4}$)-$\sqrt{3}$cos2x+1
=cos(2x-$\frac{π}{2}$)-$\sqrt{3}$cos2x+2=sin2x-$\sqrt{3}$cos2x+2=2sin(2x-$\frac{π}{3}$)+2,
對稱軸方程是$x=\frac{k}{2}π+\frac{5}{12}π(k∈Z)$;
(2)由(1)得:f(x)=2sin(2x-$\frac{π}{3}$)+2.
∵x∈[$\frac{π}{4}$,$\frac{π}{2}$],∴2x-$\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],
∴當2x-$\frac{π}{3}$=$\frac{π}{6}$,即x=$\frac{π}{4}$時,fmin(x)=3.
當2x-$\frac{π}{3}$=$\frac{π}{2}$,即x=$\frac{5π}{12}$時,fmax(x)=4;
(3)|f(x)-m|<2?m-2<f(x)<m+2,
∵對任意實數x,不等式|f(x)-m|<2在x∈[$\frac{π}{4}$,$\frac{π}{2}$]上恒成立,
∴$\left\{\begin{array}{l}{m-2{<f(x)}_{min}}\\{m+2{>f(x)}_{max}}\end{array}\right.$,即 $\left\{\begin{array}{l}{m-2<3}\\{m+2>4}\end{array}\right.$,解得:2<m<5.
故m的取值范圍為(2,5).
點評 本題考查了三角函數倍角公式,兩角差的正弦公式,考查了三角函數最值的求法,考查了數學轉化思想方法,關鍵是把不等式恒成立問題轉化為含m的代數式與f(x)的最值關系問題,是中檔題.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $\frac{{\sqrt{3}}}{8}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
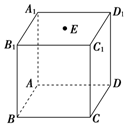 如圖,已知正方體ABCD-A1B1C1D1中,點E是上底面A1C1的中心,化簡下列向量表達式,并在圖中標出化簡結果的向量.
如圖,已知正方體ABCD-A1B1C1D1中,點E是上底面A1C1的中心,化簡下列向量表達式,并在圖中標出化簡結果的向量.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
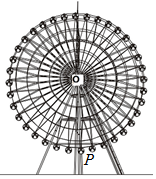 如圖所示,游樂場中的摩天輪勻速逆時針旋轉,每轉一圈需要6min,其中心O距離地面40.5m,摩天輪的半徑為40m,已知摩天輪上點P的起始位置在最低點處,在時刻t(min)時點P距離地面的高度為f(t)=Asin(ωt+φ)+h(A>0,ω>0,-π<φ<0,t≥0).
如圖所示,游樂場中的摩天輪勻速逆時針旋轉,每轉一圈需要6min,其中心O距離地面40.5m,摩天輪的半徑為40m,已知摩天輪上點P的起始位置在最低點處,在時刻t(min)時點P距離地面的高度為f(t)=Asin(ωt+φ)+h(A>0,ω>0,-π<φ<0,t≥0).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | l∥α,α⊥β⇒l⊥α | B. | l⊥α,α⊥β⇒l∥α | C. | l∥α,α∥β⇒l∥β | D. | l⊥α,α∥β⇒l⊥β |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x2+$\frac{y^2}{2}$=1 | B. | $\frac{x^2}{2}$+y2=1 | C. | x2+$\frac{y^2}{4}$=1 | D. | $\frac{x^2}{4}$+y2=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{b}{a}$<$\frac{a}{b}$ | B. | $\frac{1}{a{b}^{2}}$<$\frac{1}{{a}^{2}b}$ | C. | a2<b2 | D. | ab2<a2b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com