

分析 可以看到第三行起每一行空心圓點的個數都是前兩行空心圓點個數的和,由此可以得到一個遞推關系,利用此遞推關系求解即可.
解答 解:由題意及圖形知不妨構造這樣一個數列{an}表示空間心圓點的個數變化規律,令a1=1,a2=0,n≥3時,an=an-1+an-2,本數列中的n對應著圖形中的第n行中空心圓點的個數.由此知a10即所求.
故各行中空心圓點的個數依次為1,0,1,1,2,3,5,8,13,21,34,55,89,..
a10=21,即第10行中空心圓點的個數是21
故答案為:21.
點評 本題主要考查了數列的應用,解題的關鍵構造這樣一個數列{an}表示空間心圓點的個數變化規律,令a1=1,a2=0,n≥3時,an=an-1+an-2,屬于中檔題.


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -2i | C. | 2 | D. | 2i |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
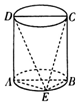
| A. | AE⊥CE | B. | BE⊥DE | C. | DE⊥CE | D. | 面ADE⊥面BCE |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖所示,為測量山高MN,選擇A和另一座山的山頂C為測量觀測點,從A測得M點的仰角∠MAN=60°,C點的仰角∠CAB=30°,以及∠MAC=105°,從C測得∠MCA=45°,已知山高BC=150米,則所求山高MN為150$\sqrt{6}$m.
如圖所示,為測量山高MN,選擇A和另一座山的山頂C為測量觀測點,從A測得M點的仰角∠MAN=60°,C點的仰角∠CAB=30°,以及∠MAC=105°,從C測得∠MCA=45°,已知山高BC=150米,則所求山高MN為150$\sqrt{6}$m.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充要條件 | B. | 充分不必要條件 | ||
| C. | 必要不充分條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-6) | B. | (-∞,-6)∪(6,+∞) | C. | (6,+∞) | D. | (-6,6) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com