
| A. | (-∞,-6) | B. | (-∞,-6)∪(6,+∞) | C. | (6,+∞) | D. | (-6,6) |
分析 原方程等價于x3+a=$\frac{4}{x}$,原方程的實根是曲線y=x3+a與曲線y=$\frac{4}{x}$的交點的橫坐標:分a>0與a<0討論,利用數形結合即可得到結論.
解答 解:方程的根顯然x≠0,原方程等價于x3+a=$\frac{4}{x}$,
原方程的實根是曲線y=x3+a與曲線y=$\frac{4}{x}$的交點的橫坐標;
而曲線y=x3+a是由曲線y=x3向上或向下平移|a|個單位而得到的.
若交點(xi,$\frac{4}{{x}_{i}}$)(i=1,2,k)均在直線y=x的同側,
因直線y=x3與y=$\frac{4}{x}$交點為:(-2,-2),(2,2);

所以結合圖象可得:$\left\{\begin{array}{l}{a>0}\\{{x}^{3}+a>-2}\\{x≥-2}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{{x}^{3}+a<2}\\{x≤2}\end{array}\right.$
解得a>6或a<-6,即實數a的取值范圍是(-∞,-6)∪(6,∞),
故選:B
點評 本題考查函數與方程的綜合運用,利用數形結合是解決本題的關鍵.注意合理地進行等價轉化.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案科目:高中數學 來源: 題型:填空題

查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,點M($\sqrt{3}$,$\sqrt{2}$)在橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且點M到兩焦點的距離之和為6.
如圖,點M($\sqrt{3}$,$\sqrt{2}$)在橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且點M到兩焦點的距離之和為6.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
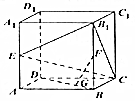 如圖,在長方體ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分別是AA1和BB1的中點,G是DB上的點,且DG=2GB.
如圖,在長方體ABCD-A1B1C1D1中,AB=$\sqrt{3}$,AA1=2,AD=1,E、F分別是AA1和BB1的中點,G是DB上的點,且DG=2GB.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com