
 如圖,正方體ABCD-A1B1C1D1的棱長為a,在此幾何體中,給出下面四個結論:①異面直線A1D與AB1所成角為60°;②直線A1D與BC1垂直;③直線A1D與BD1平行;④三棱錐A-A1CD的體積為$\frac{1}{6}{a^3}$,其中正確的結論個數是( )
如圖,正方體ABCD-A1B1C1D1的棱長為a,在此幾何體中,給出下面四個結論:①異面直線A1D與AB1所成角為60°;②直線A1D與BC1垂直;③直線A1D與BD1平行;④三棱錐A-A1CD的體積為$\frac{1}{6}{a^3}$,其中正確的結論個數是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根據題意,求出異面直線A1D與AB1所成的角,判斷①正確;
判斷異面直線A1D與BC1垂直,得出②正確;
求出異面直線A1D與BD1所成的角,判斷③錯誤;
求出三棱錐A-A1CD的體積,判斷④正確.
解答 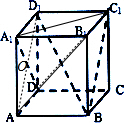 解:如圖所示,正方體ABCD-A1B1C1D1中,棱長為a,
解:如圖所示,正方體ABCD-A1B1C1D1中,棱長為a,
對于①,連接DC1,A1C1,則△A1C1D是正三角形,∠A1DC1是異面直線
A1D與AB1所成的角,為60°,①正確;
對于②,連接AD1,則∠AOA1是異面直線A1D與BC1所成的角,且AD1⊥A1D,
∴異面直線A1D與BC1垂直,②正確;
對于③,直線A1D與BD1是異面直線,異面直線所成的角是60°,∴③錯誤;
對于④,三棱錐A-A1CD的體積為V=$\frac{1}{3}$•$\frac{1}{2}$•a•$\sqrt{2}$a•$\frac{1}{2}$•$\sqrt{2}$a=$\frac{1}{6}{a^3}$,∴④正確.
綜上,正確的命題序號是①②④,共3個.
故選:C.
點評 本題考查了空間中的平行與異面直線所成的角的應用問題,是綜合題.


 優學名師名題系列答案
優學名師名題系列答案科目:高中數學 來源: 題型:選擇題
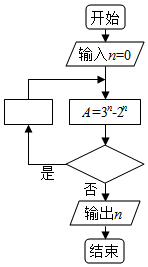 如圖程序框圖是為了求出滿足3n-2n>1000的最小偶數n,那么在
如圖程序框圖是為了求出滿足3n-2n>1000的最小偶數n,那么在 和
和 兩個空白框中,可以分別填入( )
兩個空白框中,可以分別填入( )| A. | A>1000和n=n+1 | B. | A>1000和n=n+2 | C. | A≤1000和n=n+1 | D. | A≤1000和n=n+2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,2) | B. | (0,1) | C. | (-1,0) | D. | (1,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -$\frac{3}{2}$ | C. | -$\frac{4}{3}$ | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com