
分析 (1)由圓C的方程求出圓心坐標和半徑,設出M坐標,由$\overrightarrow{CM}$與$\overrightarrow{MP}$數量積等于0列式得M的軌跡方程;
(2)設M的軌跡的圓心為N,由|OP|=|OM|得到ON⊥PM.求出ON所在直線的斜率,由直線方程的點斜式得到PM所在直線方程,由點到直線的距離公式求出O到l的距離,再由弦心距、圓的半徑及弦長間的關系求出PM的長度,代入三角形面積公式得答案;
(3)將直線與圓方程聯立組成方程組,求出方程組的解得到兩交點A與B的坐標,當圓面積最小時,弦AB為直徑,利用兩點間的距離公式求出|AB|的長,即為圓的直徑,確定出圓的半徑,利用線段中點坐標公式求出線段AB的中點坐標,即為圓心坐標,由圓心坐標和半徑寫出圓的標準方程即可.
解答 解:(1)圓C的方程可化為x2+(y-4)2=16,
所以圓心為C(0,4),半徑為4.
設M(x,y),則$\overrightarrow{CM}$=(x,y-4),$\overrightarrow{MP}$=(2-x,2-y).
由題設知$\overrightarrow{CM}$•$\overrightarrow{MP}$=0,故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.
由于點P在圓C的內部,所以M的軌跡方程是(x-1)2+(y-3)2=2.
(2)由(1)可知M的軌跡是以點N(1,3)為圓心,$\sqrt{2}$為半徑的圓.
由于|OP|=|OM|,故O在線段PM的垂直平分線上,又P在圓N上,從而ON⊥PM.
因為ON的斜率為3,所以直線l的斜率為-$\frac{1}{3}$,
故l的方程為y=-$\frac{1}{3}$x+$\frac{8}{3}$.
又|OM|=|OP|=2 $\sqrt{2}$,O到直線l的距離為$\frac{4\sqrt{10}}{5}$,
故|PM|=$\frac{4\sqrt{10}}{5}$,所以△POM的面積為$\frac{16}{5}$.
(3)聯立y=-$\frac{1}{3}$x+$\frac{8}{3}$與圓C:x2+y2-8y=0
得:5y2-28y+32=0,
解得:y1=4,y2=$\frac{8}{5}$,
當弦AB為直徑時,圓面積最小,
則所求圓的直徑為2R=|AB|=$\sqrt{1+9}•|4-\frac{8}{5}|$=$\frac{12\sqrt{10}}{5}$,
圓心為AB中點C(-$\frac{2}{5}$,$\frac{14}{5}$),
則所求面積最小的圓的方程是(x+$\frac{2}{5}$)2+(y-$\frac{14}{5}$)2=$\frac{72}{5}$.
點評 本題考查圓的軌跡方程的求法,訓練了利用向量數量積判斷兩個向量的垂直關系,訓練了點到直線的距離公式的應用,是中檔題.


 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | (0,$\sqrt{5}$) | B. | (-$\sqrt{5}$,0) | C. | (-$\sqrt{13}$,0) | D. | (0,5) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
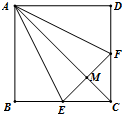 如圖,正方形ABCD中,E,F分別是BC,CD的中點,M是EF的中點,現在沿AE,AF及EF把這個正方形折成一個四面體,使B,C,D三點重合,重合后的點記為P,則在四面體A-PEF中必有( )
如圖,正方形ABCD中,E,F分別是BC,CD的中點,M是EF的中點,現在沿AE,AF及EF把這個正方形折成一個四面體,使B,C,D三點重合,重合后的點記為P,則在四面體A-PEF中必有( )| A. | PM⊥△AEF所在平面 | B. | AM⊥△PEF所在平面 | C. | PF⊥△AEF所在平面 | D. | AP⊥△PEF所在平面 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {-2-$\sqrt{7}$,1,3} | B. | {2-$\sqrt{7}$,1,3} | C. | {-3,-1,1,3} | D. | {1,3} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
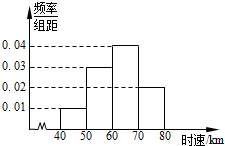 為了解某一段公路汽車通過時的車速情況,現隨機抽測了通過這段公路的200輛汽車的時速,所得數據均在區間[40,80]中,其頻率分布直方圖如圖所示,則在抽測的200輛汽車中,時速在區間[40,60)內的汽車有80輛.
為了解某一段公路汽車通過時的車速情況,現隨機抽測了通過這段公路的200輛汽車的時速,所得數據均在區間[40,80]中,其頻率分布直方圖如圖所示,則在抽測的200輛汽車中,時速在區間[40,60)內的汽車有80輛.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com