Question

4．在邊長為1的正方形ABCD中，向量$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{DC}$，$\overrightarrow{BF}$=$\frac{1}{3}$$\overrightarrow{BC}$，則向量$\overrightarrow{AE}$，$\overrightarrow{AF}$的夾角為（　　）

• A． $\frac{π}{6}$
• B． $\frac{π}{4}$
• C． $\frac{π}{3}$
• D． $\frac{5π}{12}$

Answer 1

分析 以A為坐標原點，以AB為x軸，以AD為x軸，建立直角坐標系，根據向量的夾角的公式計算即可

解答 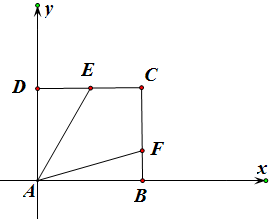解：設向量$\overrightarrow{AE}$，$\overrightarrow{AF}$的夾角為θ，
以A為坐標原點，以AB為x軸，以AD為x軸，建立直角坐標系，
∴A（0，0），B（1.0），C（1，1），D（0，1），
∵向量$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{DC}$，$\overrightarrow{BF}$=$\frac{1}{3}$$\overrightarrow{BC}$，
∴E（$\frac{1}{2}$，1），F（1，$\frac{1}{3}$），
∴$\overrightarrow{AE}$=（$\frac{1}{2}$，1），$\overrightarrow{AF}$=（1，$\frac{1}{3}$），
∴|$\overrightarrow{AE}$|=$\sqrt{\frac{5}{4}}$，$\overrightarrow{AF}$=$\sqrt{\frac{10}{9}}$，$\overrightarrow{AE}$•$\overrightarrow{AF}$=$\frac{1}{2}$+$\frac{1}{3}$=$\frac{5}{6}$，
∴cosθ=$\frac{\overrightarrow{AE}•\overrightarrow{AF}}{|\overrightarrow{AE}|•|\overrightarrow{AF}|}$=$\frac{\frac{5}{6}}{\sqrt{\frac{5}{4}×\frac{10}{9}}}$=$\frac{\sqrt{2}}{2}$，
∴θ=$\frac{π}{4}$，
故選：B

點評 本題考查了向量的坐標運算和向量的夾角公式，屬于中檔題．