
分析 由條件求得α、β的范圍,可得α+2β的范圍,再求得tanβ、tan2β、tan(α+2β)的值,從而求得α+2β的值.
解答 解:(1)∵$α∈({0,\frac{π}{2}}),β∈({0,\frac{π}{2}})$,且$tanα=\frac{1}{7},sinβ=\frac{{\sqrt{10}}}{10}$,∴α∈( 0,$\frac{π}{4}$)、β∈(0,$\frac{π}{6}$),
∴α+2β∈(0,$\frac{7π}{12}$),且cosβ=$\sqrt{{1-sin}^{2}β}$=$\frac{3\sqrt{10}}{10}$,∴tanβ=$\frac{1}{3}$,tan(2β)=$\frac{2tanβ}{1{-tan}^{2}β}$=$\frac{3}{4}$,
∴tan(α+2β)=$\frac{tanα+tan2β}{1-tanα•tan2β}$=$\frac{\frac{1}{7}+\frac{3}{4}}{1-\frac{1}{7}•\frac{3}{4}}$=1,∴α+2β=$\frac{π}{4}$.
(2)∵$α∈({-π,0}),β∈({0,\frac{π}{2}})$,且$tanα=\frac{1}{7},sinβ=\frac{{\sqrt{10}}}{10}$,∴α∈(-π,-$\frac{5π}{6}$)、β∈(0,$\frac{π}{6}$),
∴α+2β∈(-π,-$\frac{π}{2}$),且cosβ=$\sqrt{{1-sin}^{2}β}$=$\frac{3\sqrt{10}}{10}$,∴tanβ=$\frac{1}{3}$,tan(2β)=$\frac{2tanβ}{1{-tan}^{2}β}$=$\frac{3}{4}$,
∴tan(α+2β)=$\frac{tanα+tan2β}{1-tanα•tan2β}$=$\frac{\frac{1}{7}+\frac{3}{4}}{1-\frac{1}{7}•\frac{3}{4}}$=1,∴α+2β=-$\frac{3π}{4}$.
點評 本題主要考查同角三角函數的基本關系,誘導公式,兩角和差的三角公式,以及三角函數在各個象限中的符號,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
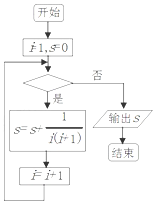 一個算法的框圖如右圖所示,若該程序輸出的結果為$\frac{5}{6}$,則判斷框中應填入的條件是( )
一個算法的框圖如右圖所示,若該程序輸出的結果為$\frac{5}{6}$,則判斷框中應填入的條件是( )| A. | i<6 | B. | i≤6 | C. | i<5 | D. | i≤7 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $f({\frac{{{x_1}+{x_2}}}{2}})<\frac{{f({x_1})+f({x_2})}}{2}$ | B. | $f({\frac{{{x_1}+{x_2}}}{2}})>\frac{{f({x_1})+f({x_2})}}{2}$ | ||
| C. | $f({\frac{{{x_1}+{x_2}}}{2}})=\frac{{f({x_1})+f({x_2})}}{2}$ | D. | 無法確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | c<b<a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com