
| A. | $f({\frac{{{x_1}+{x_2}}}{2}})<\frac{{f({x_1})+f({x_2})}}{2}$ | B. | $f({\frac{{{x_1}+{x_2}}}{2}})>\frac{{f({x_1})+f({x_2})}}{2}$ | ||
| C. | $f({\frac{{{x_1}+{x_2}}}{2}})=\frac{{f({x_1})+f({x_2})}}{2}$ | D. | 無法確定 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
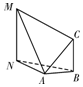 如圖,為測量山高MN,選擇A和另一座山的山頂C為測量觀測點.從M點測得A點的俯角∠NMA=30°,C點的仰角∠CAB=45°以及∠MAC=75°;從C點測得∠MCA=60°;已知山高BC=200m,則山高MN=( )
如圖,為測量山高MN,選擇A和另一座山的山頂C為測量觀測點.從M點測得A點的俯角∠NMA=30°,C點的仰角∠CAB=45°以及∠MAC=75°;從C點測得∠MCA=60°;已知山高BC=200m,則山高MN=( )| A. | 300m | B. | 200$\sqrt{2}$m | C. | 200$\sqrt{3}$m | D. | 300$\sqrt{2}$m |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[{\frac{1}{13},2}]$ | B. | [$\frac{2}{13}$,1] | C. | $[{\frac{1}{6},6}]$ | D. | $[{\frac{1}{3},3}]$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com