
分析 (1)f′(x)=(x2+2x+1-a)ex,令u(x)=x2+2x+1-a=(x+1)2-a.u(-1)=-a,u(-2)=1-a,u(2)=9-a.由函數(shù)f(x)在區(qū)間[-2,2]上是單調(diào)函數(shù),可得u(x)≤0,或u(x)≥0,x∈[-2,2].利用二次函數(shù)的單調(diào)性即可得出.
(2)f(x)有兩個不同的極值點m,n(m<n),即u(x)=x2+2x+1-a=(x+1)2-a=0有兩個不等的實數(shù)根m,n.可得-a<0,且m+n=-2,mn=1-a.再根據(jù)2(m+n)≤mn-1,可得0<a≤4.另一方面:m=-1-$\sqrt{a}$.F(x)=e2f(x)+g(x)=ex+2(2x2-a-1),F(xiàn)(m)=em+2(2m2-a-1)=${e}^{1-\sqrt{a}}$$(a+4\sqrt{a}+1)$,令$\sqrt{a}$=t∈(0,2].令h(t)=e1-t(t2+4t-1),t∈(0,2].利用導(dǎo)數(shù)研究其單調(diào)性極值與最值即可得出.
解答 解:(1)f′(x)=(x2+2x+1-a)ex,
令u(x)=x2+2x+1-a=(x+1)2-a.
u(-1)=-a,u(-2)=1-a,u(2)=9-a.
∵函數(shù)f(x)在區(qū)間[-2,2]上是單調(diào)函數(shù),∴u(x)≤0,或u(x)≥0,x∈[-2,2].
∴9-a≤0,或-a≥0,
解得a≥9,或a≤0.
∴a≥9時,u(x)≤0,f′(x)≤0,函數(shù)f(x)在x∈[-2,2]上單調(diào)遞減.
a≤0時,u(x)≥0,f′(x)≥0,函數(shù)f(x)在x∈[-2,2]上單調(diào)遞增.
(2)∵f(x)有兩個不同的極值點m,n(m<n),
∴u(x)=x2+2x+1-a=(x+1)2-a=0有兩個不等的實數(shù)根m,n.
∴-a<0,解得a>0.
且m+n=-2,mn=1-a.
∵2(m+n)≤mn-1,
∴-4≤1-a-1,解得a≤4.
∴0<a≤4.
另一方面:m=-1-$\sqrt{a}$.
F(x)=e2f(x)+g(x)=e2•(x2-a+1)ex+(x2-2)ex+2=ex+2(2x2-a-1),
F(m)=em+2(2m2-a-1)=${e}^{1-\sqrt{a}}$$(a+4\sqrt{a}+1)$,令$\sqrt{a}$=t∈(0,2].
則h(t)=e1-t(t2+4t-1),t∈(0,2].
h′(t)=$\frac{-e({t}^{2}+2t-5)}{{e}^{t}}$=$\frac{-e[t+(1+\sqrt{6})][t-(\sqrt{6}-1)]}{{e}^{t}}$,
∴h(t)在(0,$\sqrt{6}$-1]上單調(diào)遞增,在($\sqrt{6}$-1,2]上單調(diào)遞減.
h(0)=-e,h(2)=$\frac{7}{e}$,$h(\sqrt{6}-1)$=2+2$\sqrt{6}$.
∴h(t)∈$(-e,2+2\sqrt{6}]$.
即F(m))∈$(-e,2+2\sqrt{6}]$.
點評 本題考查了利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性極值與最值、方程與不等式的解法,考查了推理能力與計算能力,屬于難題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | [1,+∞) | B. | (0,1] | C. | [$\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
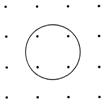 如圖所示,在排成4×4方陣的16個點中,中心位置4個點在某圓內(nèi),其余12個點在圓外.從16個點中任選3點,作為三角形的頂點,其中至少有一個頂點在圓內(nèi)的三角形共有312個.
如圖所示,在排成4×4方陣的16個點中,中心位置4個點在某圓內(nèi),其余12個點在圓外.從16個點中任選3點,作為三角形的頂點,其中至少有一個頂點在圓內(nèi)的三角形共有312個.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
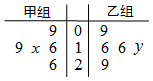 如圖所示莖葉圖記錄了甲、乙兩組各五名學(xué)生在一次英語聽力測試中的成績(單位:分),已知甲組數(shù)據(jù)的中位數(shù)為17,乙組數(shù)據(jù)的平均數(shù)為17.4,則x、y的值分別為( )
如圖所示莖葉圖記錄了甲、乙兩組各五名學(xué)生在一次英語聽力測試中的成績(單位:分),已知甲組數(shù)據(jù)的中位數(shù)為17,乙組數(shù)據(jù)的平均數(shù)為17.4,則x、y的值分別為( )| A. | 7、8 | B. | 5、7 | C. | 8、5 | D. | 7、7 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com