
分析 (Ⅰ)通過等比數列的通項公式可知an+1-2an=2n,兩端同除2n+1即得結論;
(Ⅱ)利用錯位相減法計算即得結論,
(Ⅲ)利用放縮法即可證明.
解答 解:(Ⅰ)證明:由已知得${a_{n+1}}-2{a_n}=({a_2}-2{a_1})•{2^{n-1}}={2^n}$,
兩端同除2n+1得:$\frac{{{a_{n+1}}}}{{{2^{n+1}}}}-\frac{a_n}{2^n}=\frac{1}{2}$,
所以數列$\{\frac{a_n}{2^n}\}$是以首項為$\frac{1}{2}$,公差為$\frac{1}{2}$的等差數列;
(Ⅱ)由(Ⅰ)知$\frac{a_n}{2^n}=\frac{1}{2}n$,所以${a_n}=n•{2^{n-1}}$,
${S_n}=1•{2^0}+2•{2^1}+…+n•{2^{n-1}}$,
則2Sn=1•21+2•22+…+n•2n,
相減得:$-{S_n}=1•{2^0}+{2^1}+…+{2^{n-1}}-n•{2^n}$,
所以$-{S_n}=\frac{{1-{2^n}}}{1-2}-n•{2^n}$,
即${S_n}=(n-1){2^n}+1$.
(Ⅲ)證明:數列cn=2n-2,n≥2,
∴$\frac{1}{c_n}=\frac{1}{{{2^n}-2}}>\frac{1}{2^n}$,
∴$\frac{1}{c_2}+\frac{1}{c_3}+…+\frac{1}{c_n}>\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}=\frac{{\frac{1}{4}[1-{{(\frac{1}{2})}^{n-1}}]}}{{1-\frac{1}{2}}}=\frac{1}{2}-{(\frac{1}{2})^n}$
又∵$\frac{1}{c_n}=\frac{1}{{{2^n}-2}}<\frac{2}{2^n}={(\frac{1}{2})^{n-1}}$,(n≥3),
當n=2時,$\frac{1}{c_2}=\frac{1}{2}$,
∴$\frac{1}{{c}_{2}}+\frac{1}{{c}_{3}}+…+\frac{1}{{c}_{n}}$<$\frac{1}{{2}^{1}}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}}$=$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n-1}]}{1-\frac{1}{2}}$=1-($\frac{1}{2}$)n-1,
所以原不等式得證.
點評 本題考查數列的通項及前n項和不等式的證明,對表達式的靈活變形及錯位相減法和放縮是解決本題的關鍵,注意解題方法的積累,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
 “牟合方蓋”是我國古代數學家劉微在研究球的體積的過程中構造的一個和諧優(yōu)美的幾何體,它由完全相同的四個曲面構成,相對的兩個曲面在同一圓柱的側面上,好似兩個扣合(牟合)在一起的方形傘(方蓋).如圖,正邊形ABCD是為體現其直觀性所作的輔助線,若該幾何體的正視圖與側視圖都是半徑為r的圓,根據祖暅原理,可求得該幾何體的體積為( )
“牟合方蓋”是我國古代數學家劉微在研究球的體積的過程中構造的一個和諧優(yōu)美的幾何體,它由完全相同的四個曲面構成,相對的兩個曲面在同一圓柱的側面上,好似兩個扣合(牟合)在一起的方形傘(方蓋).如圖,正邊形ABCD是為體現其直觀性所作的輔助線,若該幾何體的正視圖與側視圖都是半徑為r的圓,根據祖暅原理,可求得該幾何體的體積為( )| A. | $\frac{8}{3}{r^3}$ | B. | $\frac{8}{3}π{r^3}$ | C. | $\frac{16}{3}{r^3}$ | D. | $\frac{16}{3}π{r^3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
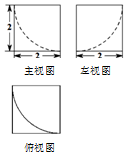
| A. | $8-\frac{4}{3}π$ | B. | $8-\frac{8}{3}π$ | C. | 24-π | D. | 24+π |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | 1或$\frac{1}{2}$ | D. | 無法確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com