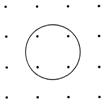
如圖所示，在排成4×4方陣的16個點中，中心位置4個點在某圓內，其余12個點在圓外．從16個點中任選3點，作為三角形的頂點，其中至少有一個頂點在圓內的三角形共有312個． 分析 根據題意，按圓內取出的點的數目分3種情況討論：①、取出的3個點都在圓內，②、在圓內取2點，圓外12點中取1點，③、在圓內取1點，圓外12點中取2點，分別求出每一種情況的取法數目，由分類計數原理計算可得答案．
解答 解：根據題意，分3種情況討論：
①、取出的3個點都在圓內，有C43=4種取法，即有4種取法，
②、在圓內取2點，圓外12點中取1點，有C42C101=60種，即有60種取法，
③、在圓內取1點，圓外12點中取2點，有C41（C122-4）=248種，即有248種取法，
則至少有一個頂點在圓內的三角形有4+60+248=312個，
故答案為：312．
點評 本題考查排列、組合的實際應用，注意要分類討論，要做到不重不漏．
科目：高中數學 來源： 題型：選擇題
| A． | n+（n+1）+（n+2）+…+（3n-2）=n2 | B． | n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2 | ||
| C． | n+（n+1）+（n+2）+…+（3n-1）=n2 | D． | n+（n+1）+（n+2）+…+（3n-1）=（2n-1）2 |
查看答案和解析>>
科目：高中數學 來源： 題型：填空題
查看答案和解析>>
科目：高中數學 來源： 題型：選擇題
| A． | 0 | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{2}$ |
查看答案和解析>>
科目：高中數學 來源： 題型：填空題
查看答案和解析>>
科目：高中數學 來源： 題型：選擇題
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
查看答案和解析>>
科目：高中數學 來源： 題型：選擇題
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | -$\frac{{\sqrt{3}}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com