
分析 (I)利用已知條件求出數列的公差,然后求{an}的通項公式;
(II)化簡數列的表達式,利用裂項消項法求解數列的和即可.
解答 (每小題(6分),共12分)
解:(I)由a1=10,a2為整數知,等差數列{an}的公差d為整數.
又Sn≤S4,故a4≥0,a5≤0,(2分)
于是10+3d≥0,10+4d≤0,解得$-\frac{10}{3}≤d≤-\frac{5}{2}$,因此d=-3,(4分)
故數列{an}的通項公式為an=13-3n. (6分)
(II)∵${b_n}=\frac{1}{{({13-3n})({10-3n})}}=\frac{1}{3}({\frac{1}{10-3n}-\frac{1}{13-3n}})$,(8分)
于是Tn=b1+b2+b3+…+bn
=$\frac{1}{3}[(\frac{1}{7}-\frac{1}{10})+(\frac{1}{4}-\frac{1}{7})+…+(\frac{1}{10-3n}-\frac{1}{12-3n})]$
=$\frac{1}{3}(\frac{1}{10-3n}-\frac{1}{10})$
=$\frac{n}{10(10-3n)}$.(12分)
點評 本題考查數列的遞推關系式的應用,數列求和,考查計算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2ln2 | B. | ln2+1 | C. | ln2 | D. | ln2-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
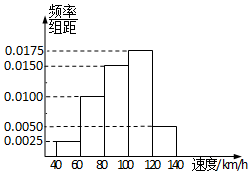 根據某固定測速點測得的某時段內過往的200輛機動車的行駛速度(單位:km/h)繪制的頻率分布直方圖如圖所示.該路段限速標志牌提示機動車輛正常行駛速度為60km/h-120km/h,則該時段內非正常行駛的機動車輛數為30.
根據某固定測速點測得的某時段內過往的200輛機動車的行駛速度(單位:km/h)繪制的頻率分布直方圖如圖所示.該路段限速標志牌提示機動車輛正常行駛速度為60km/h-120km/h,則該時段內非正常行駛的機動車輛數為30.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com