
分析 (1)由題意,當a=1時,可得f(x)=$lo{g}_{\frac{1}{2}}({4}^{x}+{2}^{x}-1)=-x$,x∈[0,1],可得函數f(x)的準不動點.
(2)依題意,“f(x)在區間D上有不動點”當且僅當“F(x)=f(x)+x在區間D上有零點”,F(x)在區間[0,1]上是一條連續不斷的曲線,換元法轉化為二次函數問題求解準不動點,可得實數a的取值范圍.
解答 解:(1)由題意,當a=1時,可得f(x)=$lo{g}_{\frac{1}{2}}({4}^{x}+{2}^{x}-1)=-x$,x∈[0,1],
可得:4x+2x-1=2x,
即4x=1
∴x=0.
當a=1,函數f(x)的準不動點為x0=0.
(2)由定義:f(x)=$lo{g}_{\frac{1}{2}}({4}^{x}+a{2}^{x}-1)=-x$,x∈[0,1],上有零點”,
可得:F(x)=4x+a•2x-1-2x,即F(x)=(2x)2+a•2x-1-2x,上有零點”,
且4x+a•2x-1>0,
令2x=t,
x∈[0,1],
則t∈[1,2]
那么F(x)轉化為g(x)=t2+at-t-1,上有零點”圖象是一條連續不斷的曲線,
且t2+at-1>0,(1≤t≤2).
根據二次函數根的分布:則有$\left\{\begin{array}{l}{g(1)≤0}\\{g(2)≥0}\end{array}\right.$或$\left\{\begin{array}{l}{g(1)≥0}\\{g(2)≤0}\end{array}\right.$.
解得$-\frac{1}{2}≤a≤1$.
要使t2+at-1>0(1≤t≤2)恒成立.
其對稱軸x=$-\frac{a}{2}$,在1≤t≤2上是遞增的,當t=1時最小值,
可得a>0.
綜上可得實數a的取值范圍是(0,1].
點評 本題主要考查了函數與方程的綜合運用,以及函數零點最值等有關知識,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π-2}{2}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
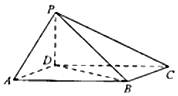 如圖,四棱錐P-ABCD中,底面ABCD為平行四邊形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如圖,四棱錐P-ABCD中,底面ABCD為平行四邊形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p1+p2+p3 | B. | 1-(1-p1)(1-p2)(1-p3) | C. | 1-p1p2p3 | D. | p1p2p3 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
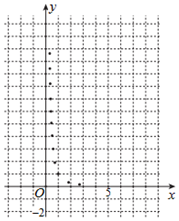 某學生為了測試煤氣灶燒水如何節省煤氣的問題設計了一個實驗,并獲得了煤氣開關旋鈕旋轉的弧度數x與燒開一壺水所用時間y的一組數據,且作了一定的數據處理(如表),得到了散點圖(如圖).
某學生為了測試煤氣灶燒水如何節省煤氣的問題設計了一個實驗,并獲得了煤氣開關旋鈕旋轉的弧度數x與燒開一壺水所用時間y的一組數據,且作了一定的數據處理(如表),得到了散點圖(如圖).| $\bar x$ | $\bar y$ | $\bar w$ | $\sum_{i=1}^{10}{({x_i}-\bar x)^2}$ | $\sum_{i=1}^{10}{({w_i}-\bar w)^2}$ | $\sum_{i=1}^{10}({x_i}-\bar x)({y_i}-\bar y)$ | $\sum_{i=1}^{10}({w_i}-\bar w)({y_i}-\bar y)$ |
| 1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com