Question

12．已知△ABC中∠C=90°，AC=4，BC=2，D是BC的中點，E是AD的中點，P是△ABD（包括邊界）內任一點，則$\overrightarrow{CP}$•$\overrightarrow{CE}$的最小值是1．

Answer 1

分析 建立平面直角坐標系，利用平面向量的坐標表示求出$\overrightarrow{CP}$•$\overrightarrow{CE}$的最小值．

解答 解：建立平面直角坐標系如圖所示，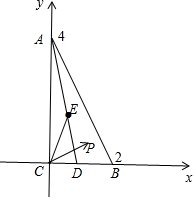
則A（0，4），B（2，0），D（1，0），
E是AD的中點，∴E（1，2）；
又P是△ABD（包括邊界）內任一點，
當P與A重合時，$\overrightarrow{CP}$•$\overrightarrow{CE}$=$\overrightarrow{CA}$•$\overrightarrow{CE}$=0×1+4×2=8，
當P與D重合時，$\overrightarrow{CP}$•$\overrightarrow{CE}$=$\overrightarrow{CD}$•$\overrightarrow{CE}$=1×1+0×2=1，
當P與B重合時，$\overrightarrow{CP}$•$\overrightarrow{CE}$=$\overrightarrow{CB}$•$\overrightarrow{CE}$=2×1+0×2=2，
當P與E重合時，$\overrightarrow{CP}$•$\overrightarrow{CE}$=$\overrightarrow{CE}$•$\overrightarrow{CE}$=1×1+2×2=5，
由此知，當P與D重合時，$\overrightarrow{CP}$•$\overrightarrow{CE}$的值最小，為1．
故答案為：1．

點評 本題考查了平面向量的數量積運算問題，是基礎題．