
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
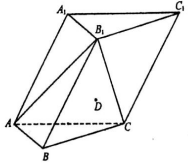 如圖,在各棱長均為2的三棱柱ABC-A1B1C1中,側面A1ACC1⊥底面ABC,∠A1AC=60°.
如圖,在各棱長均為2的三棱柱ABC-A1B1C1中,側面A1ACC1⊥底面ABC,∠A1AC=60°.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
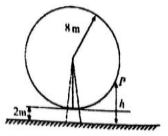 如圖,一個摩天輪的半徑為8m,每12min旋轉一周,最低點離地面為2m,若摩天輪邊緣某點P從最低點按逆時針方向開始旋轉,則點P離地面的距離h(m)與時間t(min)之間的函數關系是( )
如圖,一個摩天輪的半徑為8m,每12min旋轉一周,最低點離地面為2m,若摩天輪邊緣某點P從最低點按逆時針方向開始旋轉,則點P離地面的距離h(m)與時間t(min)之間的函數關系是( )| A. | h=8cost+10 | B. | h=-8cos$\frac{π}{3}$t+10 | C. | h=-8sin$\frac{π}{6}$t+10 | D. | h=-8cos$\frac{π}{6}$t+10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+{y^2}=1$ | C. | $\frac{x^2}{9}+\frac{y^2}{4}=1$ | D. | $\frac{x^2}{6}+\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,為測量塔高AB,選取與塔底B在同一水平面內的兩點C、D,在C、D兩點處測得塔頂A的仰角分別為45°,30°,又測得∠CBD=30°,CD=50米,則塔高AB=( )
如圖,為測量塔高AB,選取與塔底B在同一水平面內的兩點C、D,在C、D兩點處測得塔頂A的仰角分別為45°,30°,又測得∠CBD=30°,CD=50米,則塔高AB=( )| A. | 50米 | B. | 25$\sqrt{3}$米 | C. | 25米 | D. | 50$\sqrt{3}$米 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com