
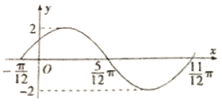
 函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分圖象如圖所示.
函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分圖象如圖所示.分析 (1)由函數的圖象的頂點坐標求出A,由周期求出ω,由五點法作圖求出φ的值,可得函數的解析式.
(2)利用函數y=Asin(ωx+φ)的圖象變換規律求得g(x)的解析式,根據條件求得sin(α+$\frac{π}{6}$)和cos(α+$\frac{π}{6}$) 的值,再利用兩角和差的三角公式、二倍角公式求得g(α)的值.
解答 解:(1)根據函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分圖象,
可得A=2,$\frac{2π}{ω}$=$\frac{11π}{12}$-(-$\frac{π}{12}$),∴ω=2,再根據五點法作圖可得2•(-$\frac{π}{12}$)+φ=0,求得φ=$\frac{π}{6}$,
∴f(x)=2sin(2x+$\frac{π}{6}$).
(2)將函數y=f(x)的圖象向右平移$\frac{π}{4}$個單位,得到函數y=g(x)=2sin(2x-$\frac{π}{2}$+$\frac{π}{6}$)=2sin(2x-$\frac{π}{3}$)的圖象,
若 f($\frac{α}{2}$)=2sin(α+$\frac{π}{6}$)=$\frac{1}{2}$,α∈($\frac{π}{3}$,$\frac{5π}{6}$),∴sin(α+$\frac{π}{6}$)=$\frac{1}{4}$.
再根據α+$\frac{π}{6}$∈($\frac{π}{2}$,π),∴cos(α+$\frac{π}{6}$)=-$\sqrt{{1-sin}^{2}(α+\frac{π}{6})}$=-$\frac{\sqrt{15}}{4}$.
則g(α)=2sin(2α-$\frac{π}{3}$)=2sin[2(α+$\frac{π}{6}$)-$\frac{2π}{3}$]=2sin(2α+$\frac{π}{3}$)cos$\frac{2π}{3}$-2cos(2α+$\frac{π}{3}$)sin$\frac{2π}{3}$
=-sin(2α+$\frac{π}{3}$)-$\sqrt{3}$•sin(2α+$\frac{π}{3}$)=-2sin(α+$\frac{π}{6}$)cos(α+$\frac{π}{6}$)-$\sqrt{3}$•(2${cos}^{2}(α+\frac{π}{6})$-1)
=-2•$\frac{1}{4}•(-\frac{\sqrt{15}}{4})$-$\sqrt{3}$•(2•$\frac{15}{16}$-1)=$\frac{\sqrt{15}-7\sqrt{3}}{8}$.
點評 本題主要考查由函數y=Asin(ωx+φ)的部分圖象求解析式,由函數的圖象的頂點坐標求出A,由周期求出ω,由五點法作圖求出φ的值;函數y=Asin(ωx+φ)的圖象變換規律,兩角和差的三角公式、二倍角的應用,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{8}{15}$ | B. | -$\frac{29}{15}$ | C. | -$\frac{27}{20}$ | D. | $\frac{1}{20}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com