
分析 (Ⅰ)將直線(xiàn)AB代入雙曲線(xiàn)方程,由題意,列不等式組,即可取得k的取值范圍;
(Ⅱ)利用弦長(zhǎng)公式求得k的值,根據(jù)向量向量的坐標(biāo)運(yùn)算,求得C點(diǎn)坐標(biāo),代入曲線(xiàn)E'上,即可求得m的值.
解答 解:(Ⅰ)設(shè)A(x1,y1),B(x2,y2),聯(lián)立方程組;$\left\{\begin{array}{l}y=kx-1\\{x^2}-{y^2}=1({x<0})\end{array}\right.$,整理得:(1-k2)x2+2kx-2=0(x<0)
從而有:$\left\{\begin{array}{l}1-{k^2}≠0\\△={({2k})^2}+8k>0\\{x_1}+{x_2}=\frac{-2k}{{1-{k^2}}}<0\\{x_1}•{x_2}=\frac{-2}{{1-{k^2}}}>0\end{array}\right.$,解得:-$\sqrt{2}$<k<-1,
∴k的取值范圍(-$\sqrt{2}$,-1);
(Ⅱ)丨AB丨=$\sqrt{1+{k}^{2}}$丨x1-x1丨=$\sqrt{1+{k}^{2}}$$\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}•{x_2}}$=$2\sqrt{\frac{{({1+{k^2}})({2-{k^2}})}}{{{{({1-{k^2}})}^2}}}}$=6$\sqrt{3}$,
整理得28k4-55k2+25=0,k2=$\frac{5}{7}$或${k^2}=\frac{5}{4}$,
注意到$-\sqrt{2}<k<-1$,所以$k=-\frac{{\sqrt{5}}}{2}$,故直線(xiàn)AB的方程為$\frac{{\sqrt{5}}}{2}x+y+1=0$,
設(shè)C(x0,y0),由已知$\overrightarrow{OA}+\overrightarrow{OB}=m\overrightarrow{OC}$,則(x1,y1)+(x2,y2)=(mx0,my0),
又${x_1}+{x_2}=\frac{-2k}{{1-{k^2}}}$=$-4\sqrt{5}$,y1+y2=k(x1+x2)-2=8,所以$C({\frac{{-4\sqrt{5}}}{m},\frac{8}{m}})$.C在曲線(xiàn)E'上,得$\frac{80}{m^2}-\frac{64}{m^2}=1$,解得:m=±4
但當(dāng)m=-4時(shí),所得的點(diǎn)在雙曲線(xiàn)的右支上,不合題意,所以m=4為所求.
點(diǎn)評(píng) 本題考查雙曲線(xiàn)的標(biāo)準(zhǔn)方程及簡(jiǎn)單幾何性質(zhì),直線(xiàn)與雙曲線(xiàn)的位置關(guān)系,考查韋達(dá)定理,弦長(zhǎng)公式,向量的坐標(biāo)運(yùn)算,考查計(jì)算能力,屬于中檔題.


 導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
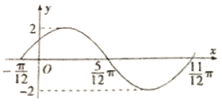 函數(shù)f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分圖象如圖所示.
函數(shù)f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分圖象如圖所示.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
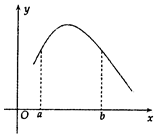 函數(shù)f(x)的圖象如圖所示,設(shè)f'(x)是f(x)的導(dǎo)函數(shù),若0<a<b,下列各式成立的是( )
函數(shù)f(x)的圖象如圖所示,設(shè)f'(x)是f(x)的導(dǎo)函數(shù),若0<a<b,下列各式成立的是( )| A. | $f'({\frac{2ab}{a+b}})<f'({\frac{a+b}{2}})<f'({\sqrt{ab}})$ | B. | $f'({\frac{2ab}{a+b}})<f'({\sqrt{ab}})<f'({\frac{a+b}{2}})$ | ||
| C. | $f'({\frac{a+b}{2}})<f'({\frac{2ab}{a+b}})<f'({\sqrt{ab}})$ | D. | $f'({\frac{a+b}{2}})<f'({\sqrt{ab}})<f'({\frac{2ab}{a+b}})$ |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com