
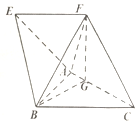
 如圖,在四棱錐A-BCFE中,四邊形EFCB為梯形,EF∥BC,且EF=$\frac{3}{4}$BC,△ABC是邊長為2的正三角形,頂點F在AC上的射影為點G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.
如圖,在四棱錐A-BCFE中,四邊形EFCB為梯形,EF∥BC,且EF=$\frac{3}{4}$BC,△ABC是邊長為2的正三角形,頂點F在AC上的射影為點G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.分析 (1)推導出FG⊥AC,取AC的中點為O,連結OB,GB,推導出FG⊥BG,FG⊥AC,從而FG⊥面ABC,由此能證明面FGB⊥面ABC.
(2)以OB所在直線為x軸,OC所在直線為y軸,過點O作平面ABC的垂線為z軸,建立空間直角坐標系,利用向量法能求出二面角E-AB-F的余弦值.
解答 證明: (1)由頂點F在AC上投影為點G,可知,FG⊥AC.
(1)由頂點F在AC上投影為點G,可知,FG⊥AC.
取AC的中點為O,連結OB,GB.
在Rt△FGC中,$FG=\sqrt{3}$,$CF=\frac{{\sqrt{21}}}{2}$,所以$CG=\frac{3}{2}$.
在Rt△GBO中,$OB=\sqrt{3}$,$OG=\frac{1}{2}$,所以$BG=\frac{{\sqrt{13}}}{2}$.
所以,BG2+GF2=FB2,即FG⊥BG.
∵FG⊥AC,FG⊥GB,AC∩BG=G
∴FG⊥面ABC.
又FG⊆面FGB,所以面FGB⊥面ABC.
解:(2)由(Ⅰ)知,OB⊥FG,OB⊥AC,且AC∩FG=G
所以 OB⊥面AFC,且FG⊥面ABC.以OB所在直線為x軸,OC所在直線為y軸,
過點O作平面ABC的垂線為z軸,建立空間直角坐標系,如圖所示:
$A(0,-1,0),B(\sqrt{3},0,0),F(0,-\frac{1}{2},\sqrt{3})$,E($\frac{3\sqrt{3}}{4}$,-$\frac{5}{4}$,$\sqrt{3}$),
$\overrightarrow{BA}=(-\sqrt{3},-1,0)$,$\overrightarrow{BE}$=(-$\frac{\sqrt{3}}{4}$,-$\frac{5}{4}$,$\sqrt{3}$),$\overrightarrow{BF}$=(-$\sqrt{3},-\frac{1}{2},\sqrt{3}$),
設平面ABE,ABF的法向量分別為$\overrightarrow{m}=(x,y,z)$,$\overrightarrow{n}=(a,b,c)$,
則$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BA}=0}\\{\overrightarrow{m}•\overrightarrow{BE}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-\sqrt{3}x-y=0}\\{-\frac{\sqrt{3}}{4}x-\frac{5}{4}y+\sqrt{3}z=0}\end{array}\right.$,取x=1,得$\overrightarrow{m}$=(1,-$\sqrt{3}$,1),
$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BA}=0\\ \overrightarrow n•\overrightarrow{BF}=0\end{array}\right.$,即$\left\{\begin{array}{l}{-\sqrt{3}a-b=0}\\{-\sqrt{3}a-\frac{1}{2}b+\sqrt{3}c=0}\end{array}\right.$,取a=1,得$\overrightarrow n=(1,-\sqrt{3},\frac{1}{2})$,
設二面角E-AB-F的平面角為θ.
則cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\frac{9}{2}}{\sqrt{5}•\sqrt{\frac{17}{4}}}$=$\frac{9\sqrt{85}}{85}$.
所以二面角E-AB-F的余弦值為$\frac{9\sqrt{85}}{85}$.
點評 本題考查面面垂直的證明,考查二面角的余弦值的求法,考查空間中線線、線面、面面間的位置關系等基礎知識,考查推理論證能力、運算求解能力、空間想象能力,考查化歸與轉化思想、數形結合思想,是中檔題.


 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:選擇題
| A. | 18 | B. | 15 | C. | 16 | D. | 25 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 24 | B. | 20 | C. | 16 | D. | 12 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,我校計劃建一個面積為200m2的矩形場地,要求矩形場地的一面利用舊墻(舊墻需要維修),其余三面圍墻要新建,在舊墻的對面的新墻上要留一個寬度為2m的進出口,已知舊墻的維修費用為41元/米,新墻的造價為400元/米.設利用舊墻的長度為x(單位:米),修建此矩形場地圍墻的總費用y(單位:元).
如圖,我校計劃建一個面積為200m2的矩形場地,要求矩形場地的一面利用舊墻(舊墻需要維修),其余三面圍墻要新建,在舊墻的對面的新墻上要留一個寬度為2m的進出口,已知舊墻的維修費用為41元/米,新墻的造價為400元/米.設利用舊墻的長度為x(單位:米),修建此矩形場地圍墻的總費用y(單位:元).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖所示的莖葉圖記錄了甲、乙兩組各5名工人某日的產量數據(單位:件).若這兩組數據的中位數相等,且平均值也相等,則x和y的值分別為( )
如圖所示的莖葉圖記錄了甲、乙兩組各5名工人某日的產量數據(單位:件).若這兩組數據的中位數相等,且平均值也相等,則x和y的值分別為( )| A. | 3,5 | B. | 5,5 | C. | 3,7 | D. | 5,7 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com