
 如圖,在直角三角形ABC中,∠B=90°,$AB=\frac{1}{2}AC=1$,點M,N分別在邊AB和AC上(M點和B點不重合),將△AMN沿MN翻折,△AMN變為△A'MN,使頂點A'落在邊BC上(A'點和B點不重合).設∠ANM=θ
如圖,在直角三角形ABC中,∠B=90°,$AB=\frac{1}{2}AC=1$,點M,N分別在邊AB和AC上(M點和B點不重合),將△AMN沿MN翻折,△AMN變為△A'MN,使頂點A'落在邊BC上(A'點和B點不重合).設∠ANM=θ分析 (1)設MA=MA'=x,則MB=1-x,在Rt△MBA'中,利用三角函數可求;
(2)求線段A'N長度的最小值,即求線段AN長度的最小值,利用三角恒等變換化簡,從而求最值.
解答 (本小題滿分12分)
解:(1)∵在直角三角形ABC中,∠B=90°,$AB=\frac{1}{2}AC=1$,
∴∠C=30°,∠BAC=60°,∠AMN=120°-θ,…(2分)
設MA=MA′=x,則MB=1-x.在Rt△MBA′中,cos∠BMA′=$\frac{1-x}{x}$,
即cos[180°-2(120°-θ)]=cos(2θ-60°)=$\frac{1-x}{x}$,
∴MA=x=$\frac{1}{1+cos(2θ-60°)}$=$\frac{1}{2co{s}^{2}(θ-30°)}$,…(5分)
∵點M在線段AB上,M點和B點不重合,A′點和B點不重合,
∴45°<120°-θ<90°,
∴30°<θ<75°. …(6分)
(2)由(1)知,在△AMN中,∠ANM=θ,∠AMN=120°-θ,
由正弦定理有$\frac{AN}{sin(120°-θ)}=\frac{AM}{sinθ}$,
∴A′N=AN=$\frac{AMsin(120°-θ)}{sinθ}$=$\frac{sin(120°-θ)}{2co{s}^{2}(θ-30°)sinθ}$ …(8分)
=$\frac{sin[90°+(30°-θ)]}{2co{s}^{2}(θ-30°)sinθ}$=$\frac{cos(30°-θ)}{2co{s}^{2}(θ-30°)sinθ}$=$\frac{1}{2cos(θ-30°)sinθ}$
=$\frac{1}{2sinθ(cosθcos30°+sinθsin30°)}$=$\frac{1}{\sqrt{3}sinθcosθ+si{n}^{2}θ}$
=$\frac{1}{\frac{1}{2}+\frac{\sqrt{3}}{2}sin2θ-\frac{1}{2}cos2θ}$=$\frac{1}{\frac{1}{2}+sin(2θ-30°)}$,…(10分)
∵30°<θ<75°,
∴30°<2θ-30°<120°,當且僅當2θ-30°=90°,
即θ=60°時,A′N有最小值$\frac{2}{3}$. …(12分)
點評 本題主要考查在實際問題中建立三角函數模型,從而利用三角函數中研究最值的方法解決最值問題,應注意角的范圍的確定是關鍵,屬于中檔題.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-1,-\frac{7}{8})$ | B. | (0,+∞) | C. | (-∞,0) | D. | $(1,\frac{6}{5})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
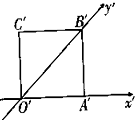 如圖,正方形O′A′B′C′的邊長為2cm,它是水平放置的一個平面圖形的直觀圖,則原平面圖形的周長是( )cm.
如圖,正方形O′A′B′C′的邊長為2cm,它是水平放置的一個平面圖形的直觀圖,則原平面圖形的周長是( )cm.| A. | 12 | B. | 16 | C. | $4(1+\sqrt{3})$ | D. | $4(1+\sqrt{2})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | 0 | C. | -1 | D. | 1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com