
分析 (1)判斷函數的奇偶性,再證明x>0的單調性,得出整個單調性;
(2)利用函數的奇偶性和單調性對不等式進行轉化,把恒成立問題轉化為最值問題.
解答 (1)因為函數f(x)的定義域為R,對于函數f(x)定義域內的每一個x,都有
f(-x)=-x+lg($\sqrt{{x}^{2}+1}-x$)=-x+lg$\frac{1}{\sqrt{{x}^{2}+1}+x}$=-f(x),.
所以,函數f(x)=x+lg$\sqrt{{x}^{2}+1}$+x)是奇函數.--(2分)
設x1,x2是(0,+∞)上任意兩個實數,且x1<x2,則
f(x1)-f(x2)=(x1-x2)+lg$\frac{\sqrt{{{x}_{1}}^{2}+1}+{x}_{1}}{\sqrt{{{x}_{2}}^{2}+1}+{x}_{2}}$..
由x1<x2,
得x1-x2<0,lg$\frac{\sqrt{{{x}_{1}}^{2}+1}+{x}_{1}}{\sqrt{{{x}_{2}}^{2}+1}+{x}_{2}}$<1.
于是f(x1)-f(x2)<0,
即f(x1)<f(x2)=(.
所以函數在(0,+∞)上是增函數,且f(x)>0,、f(0)=0,
根據奇函數的性質可得f(x)在R上的單調遞增.
(2)f(m•3x)+f(3x-9x-4)<0 等價于 m•3x<-3x+9x+4,
即 m<3x$+\frac{4}{{3}^{x}}$-1
令t=3x,設函數g(t)=t+$\frac{4}{t}$-1.
由函數g(t)的單調性可知最小值為3,
∴m<3.
∴實數m的取值范圍(-∞,3).
點評 考查了函數單調性的證明和奇偶性,單調性的綜合應用和恒成立問題的轉化思想.


科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
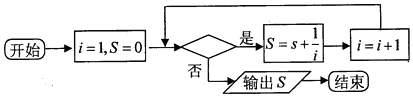
| A. | i≤2014 | B. | i>2014 | C. | i≤2013 | D. | i>2013 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
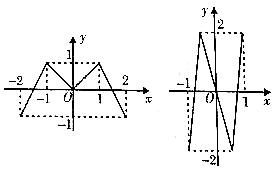 如圖,偶函數f(x)的圖象如字母M,奇函數g(x)的圖象如字母N,若方程f(g(x))=0,g(f(x))=0的實根個數分別為m、n,則m+n=( )
如圖,偶函數f(x)的圖象如字母M,奇函數g(x)的圖象如字母N,若方程f(g(x))=0,g(f(x))=0的實根個數分別為m、n,則m+n=( )| A. | 12 | B. | 18 | C. | 16 | D. | 14 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知平面ABB1N⊥平面BB1C1C,四邊形BB1C1C是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.
如圖,已知平面ABB1N⊥平面BB1C1C,四邊形BB1C1C是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{2}}{10}$ | B. | $\frac{\sqrt{5}}{10}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com