
【題目】如圖,已知四棱錐P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求證:AC⊥PB;
(2)若PB=PC= ![]() ,問在側棱PB上是否存在一點M,使得二面角M﹣AD﹣B的余弦值為
,問在側棱PB上是否存在一點M,使得二面角M﹣AD﹣B的余弦值為 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
【答案】
(1)證明:取AB的中點E,連結CE,
∵AB∥CD,DC= ![]() AB,∴DC
AB,∴DC ![]() AE,
AE,
∴四邊形AECD是平行四邊形,
又∵∠ADC=90°,∴四邊形AECD是正方形,∴CE⊥AB,
∴△CAB是等腰三角開有,且CA=CB=2,AB=2 ![]() ,
,
∴AC2+CB2=AB2,∴AC⊥CB,
又∵平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,
∴AC⊥平面PBC,
又PB平面PBC,∴AC⊥PB
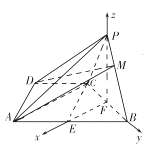
(2)解:設BC的中點為F,連結PF,
∵PB=PC,∴PF=BC,
∴PF⊥平面ABCD,∴PF⊥AC,
連結EF,則EF∥AC,∴PF⊥FE,EF⊥BC,
分別以FE、FB、FP所在的直線為x軸,y軸,z軸,建立空間直角坐標系,
∵AD=PB=PC= ![]() ,則F(0,0,0),A(2,﹣1,0),
,則F(0,0,0),A(2,﹣1,0),
B(0,1,0),D(1,﹣2,0),P(0,0,1),
∴ ![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =(﹣1,﹣1,0),
=(﹣1,﹣1,0), ![]() =(0,0,1),
=(0,0,1),
若在線段PB上存在一點M,設 ![]() =
= ![]() ,(0≤λ<1),
,(0≤λ<1),
∵ ![]() ,∴
,∴ ![]() =λ(0,1,﹣1)+(0,0,1)=(0,λ,1﹣λ),
=λ(0,1,﹣1)+(0,0,1)=(0,λ,1﹣λ),
∴M(0,λ,1﹣λ), ![]() ,
,
設平面MAD的一個法向量 ![]() =(x,y,z),
=(x,y,z),
則 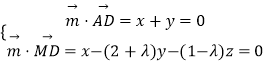 ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,
=(1,﹣1, ![]() ),
),
平面ABCD的法向量 ![]() =(0,0,1),
=(0,0,1),
∵二面角M﹣AD﹣B的余弦值為 ![]() ,
,
∴|cos< ![]() >|=
>|= ![]() =
=  =
= ![]() ,
,
解得 ![]() 或λ=2(舍).
或λ=2(舍).
∴存在點M,使得二面角M﹣AD﹣B的余弦值為 ![]() ,且
,且 ![]() =
= ![]() .
.
【解析】(1)取AB的中點E,連結CE,推導出四邊形AECD是正方形,從而CE⊥AB,再求出AC⊥CB,由此能證明AC⊥PB.(2)設BC的中點為F,連結PF,分別以FE、FB、FP所在的直線為x軸,y軸,z軸,建立空間直角坐標系,利用向量法能求出結果.
【考點精析】利用空間中直線與直線之間的位置關系對題目進行判斷即可得到答案,需要熟知相交直線:同一平面內,有且只有一個公共點;平行直線:同一平面內,沒有公共點;異面直線: 不同在任何一個平面內,沒有公共點.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 的準線
的準線![]() 與
與![]() 軸交于橢圓
軸交于橢圓![]() 的右焦點
的右焦點![]() 為
為![]() 的左焦點.橢圓的離心率為
的左焦點.橢圓的離心率為![]() ,拋物線
,拋物線![]() 與橢圓
與橢圓![]() 交于
交于![]() 軸上方一點
軸上方一點![]() ,連接
,連接![]() 并延長其交
并延長其交![]() 于點
于點![]() ,
, ![]() 為
為![]() 上一動點,且在
上一動點,且在![]() 之間移動.
之間移動.
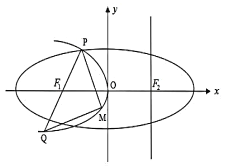
(1)當![]() 取最小值時,求
取最小值時,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的邊長恰好是三個連續的自然數,當
的邊長恰好是三個連續的自然數,當![]() 面積取最大值時,求面積最大值以及此時直線
面積取最大值時,求面積最大值以及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 C:![]() 的焦距為2,且過點
的焦距為2,且過點![]() ,右焦點為
,右焦點為![]() .設A,B 是C上的兩個動點,線段 AB 的中點M 的橫坐標為
.設A,B 是C上的兩個動點,線段 AB 的中點M 的橫坐標為![]() ,線段AB的中垂線交橢圓C于P,Q 兩點.
,線段AB的中垂線交橢圓C于P,Q 兩點.
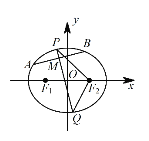
(1)求橢圓 C 的方程;
(2)設M點縱坐標為m,求直線PQ的方程,并求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知焦點在![]() 軸上的橢圓
軸上的橢圓![]() 過點
過點![]() ,且離心率為
,且離心率為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若直線![]() (
(![]() ,
,![]() )與橢圓C交于兩點A、B,點D滿足
)與橢圓C交于兩點A、B,點D滿足![]() ,經過點D及點
,經過點D及點![]() 的直線的斜率為
的直線的斜率為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖是函數y=Asin(ωx+φ)(x∈R)在區間 ![]() 上的圖象,為了得到這個函數的圖象,只要將y=sinx(x∈R)的圖象上所有的點( )
上的圖象,為了得到這個函數的圖象,只要將y=sinx(x∈R)的圖象上所有的點( ) 
A.向左平移 ![]() 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的 ![]() 倍,縱坐標不變
倍,縱坐標不變
B.向左平移 ![]() 個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
C.向左平移 ![]() 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的 ![]() 倍,縱坐標不變
倍,縱坐標不變
D.向左平移 ![]() 個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
將邊長為2的正方形ABCD沿對角線BD折疊,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=![]() .
.
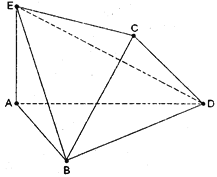
(Ⅰ)求證:DE⊥AC;
(Ⅱ)求DE與平面BEC所成角的正弦值;
(Ⅲ)直線BE上是否存在一點M,使得CM∥平面ADE,若存在,求點M的位置,不存在請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓C的長軸長為4.
,橢圓C的長軸長為4.
(1)求橢圓C的方程;
(2)已知直線![]() 與橢圓C交于A,B兩點,是否存在實數k使得以線段AB 為直徑的圓恰好經過坐標原點O?若存在,求出k的值;若不存在,請說明理由.
與橢圓C交于A,B兩點,是否存在實數k使得以線段AB 為直徑的圓恰好經過坐標原點O?若存在,求出k的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com