
【題目】(12分)已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓C的長軸長為4.
,橢圓C的長軸長為4.
(1)求橢圓C的方程;
(2)已知直線![]() 與橢圓C交于A,B兩點,是否存在實數k使得以線段AB 為直徑的圓恰好經過坐標原點O?若存在,求出k的值;若不存在,請說明理由.
與橢圓C交于A,B兩點,是否存在實數k使得以線段AB 為直徑的圓恰好經過坐標原點O?若存在,求出k的值;若不存在,請說明理由.
【答案】(1)![]() ;(2)存在實數
;(2)存在實數![]() 使得以線段AB為直徑的圓恰好經過坐標原點O.
使得以線段AB為直徑的圓恰好經過坐標原點O.
【解析】
試題本題主要考查橢圓的標準方程及其幾何性質、直線與橢圓的位置關系等基礎知識,考查學生的分析問題解決問題的能力、轉化能力、計算能力.第一問,利用橢圓的離心率和長軸長列出方程,解出a和c的值,再利用![]() 計算b的值,從而得到橢圓的標準方程;第二問,將直線與橢圓聯立,消參,利用韋達定理,得到
計算b的值,從而得到橢圓的標準方程;第二問,將直線與橢圓聯立,消參,利用韋達定理,得到![]() 、
、![]() ,由于以線段AB為直徑的圓恰好經過坐標原點O,所以
,由于以線段AB為直徑的圓恰好經過坐標原點O,所以![]() ,即
,即![]() ,代入
,代入![]() 和
和![]() ,解出k的值.
,解出k的值.
試題解析:(1)設橢圓的焦半距為c,則由題設,得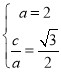 ,
,
解得 ,所以
,所以![]() ,
,
故所求橢圓C的方程為![]() .
.
(2)存在實數k使得以線段AB為直徑的圓恰好經過坐標原點O.
理由如下:
設點![]() ,
,![]() ,
,
將直線![]() 的方程
的方程![]() 代入
代入![]() ,
,
并整理,得![]() .(*)
.(*)
則![]() ,
,![]() .
.
因為以線段AB為直徑的圓恰好經過坐標原點O,
所以![]() ,即
,即![]() .
.
又![]() ,
,
于是![]() ,解得
,解得![]() ,
,
經檢驗知:此時(*)式的Δ>0,符合題意.
所以當![]() 時,以線段AB為直徑的圓恰好經過坐標原點O.
時,以線段AB為直徑的圓恰好經過坐標原點O.


 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求證:AC⊥PB;
(2)若PB=PC= ![]() ,問在側棱PB上是否存在一點M,使得二面角M﹣AD﹣B的余弦值為
,問在側棱PB上是否存在一點M,使得二面角M﹣AD﹣B的余弦值為 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,
若函數![]() 有唯一零點,則以下四個命題中正確的是______(填寫正確序號)
有唯一零點,則以下四個命題中正確的是______(填寫正確序號)
①.![]() ②.函數
②.函數![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 平行
平行
③.函數![]() 在
在![]() 上的最大值為
上的最大值為![]()
④.函數![]() 在
在 ![]() 上單調遞減
上單調遞減
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】連續拋擲同一顆均勻的骰子,令第i次得到的點數為ai , 若存在正整數k,使a1+a2+…+ak=6,則稱k為你的幸運數字.
(1)求你的幸運數字為3的概率;
(2)若k=1,則你的得分為5分;若k=2,則你的得分為3分;若k=3,則你的得分為1分;若拋擲三次還沒找到你的幸運數字則記0分,求得分X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數 ![]() .
.
(1)用含a的式子表示b;
(2)令F(x)= ![]() ,其圖象上任意一點P(x0 , y0)處切線的斜率
,其圖象上任意一點P(x0 , y0)處切線的斜率 ![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)若a=2,試求f(x)在區間 ![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線![]() 的焦點為
的焦點為![]() 上任一點
上任一點![]() 在
在![]() 軸上的射影為
軸上的射影為![]() 中點為
中點為![]() ,
,![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 過
過![]() 與
與![]() 從下到上依次交于
從下到上依次交于![]() ,與
,與![]() 交于
交于![]() ,直線
,直線![]() 過
過![]() 與
與![]() 從下到上依次交于
從下到上依次交于![]() ,與
,與![]() 交于
交于![]() ,
,![]() ,
,![]() 的斜率之積為
的斜率之積為![]() ,設
,設![]() 的面積分別為
的面積分別為![]() ,是否存在
,是否存在![]() 使得
使得![]() 成等比數列?若存在,求
成等比數列?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)=x﹣1﹣alnx,g(x)= ![]() ,a<0,且對任意x1 , x2∈[3,4](x1≠x2),|f(x1)﹣f(x2)|<|
,a<0,且對任意x1 , x2∈[3,4](x1≠x2),|f(x1)﹣f(x2)|<| ![]() ﹣
﹣ ![]() |的恒成立,則實數a的取值范圍為 .
|的恒成立,則實數a的取值范圍為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com