
分析 根據題意,將雙曲線的方程變形為標準方程,可得a=$\sqrt{4}$=2,b=$\sqrt{8}$=2$\sqrt{2}$,進而可得該雙曲線的實半軸長與虛軸長,將其相比即可得答案.
解答 解:根據題意,雙曲線的方程為2x2-y2=8,變形可得$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{8}$=1,
則有a=$\sqrt{4}$=2,b=$\sqrt{8}$=2$\sqrt{2}$,
即該雙曲線的實半軸長為2,虛軸長為2b=4$\sqrt{2}$,
則其實半軸長與虛軸長之比$\frac{a}{2b}$=$\frac{2}{4\sqrt{2}}$=$\frac{\sqrt{2}}{4}$;
故答案為:$\frac{{\sqrt{2}}}{4}$.
點評 本題考查雙曲線的幾何性質,關鍵是利用雙曲線的方程求出雙曲線的實半軸長與虛軸長.


 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 4 | C. | 3 | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,B、C在平面α的同側,M為BC的中點,若△ABC在平面α上的射影是以A為直角頂點的△AB′C′,則AM與平面α所成角的正弦值的取值范圍是( )
如圖,在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,B、C在平面α的同側,M為BC的中點,若△ABC在平面α上的射影是以A為直角頂點的△AB′C′,則AM與平面α所成角的正弦值的取值范圍是( )| A. | [$\frac{\sqrt{42}}{7}$,1) | B. | [$\frac{\sqrt{42}}{7}$,1] | C. | [$\frac{\sqrt{42}}{7}$,$\frac{\sqrt{14}}{4}$] | D. | [$\frac{\sqrt{42}}{7}$,$\frac{\sqrt{14}}{4}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x∈(0,+∞),lnx≠x-1 | B. | ?x∉(0,+∞),lnx=x-1 | ||
| C. | ?x0∈(0,+∞),lnx0≠x0-1 | D. | ?x0∉(0,+∞),lnx0=x0-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,四棱錐P-ABCD的底面ABCD為正方形,PA⊥底面ABCD,E,F分別是AC,PB的中點,PA=AB=2.
如圖,四棱錐P-ABCD的底面ABCD為正方形,PA⊥底面ABCD,E,F分別是AC,PB的中點,PA=AB=2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
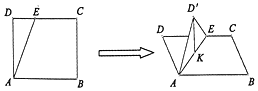 如圖,在正方形ABCD中,AB=2,E為線段CD上一動點,現將△AED沿AE折起,使點D在面ABC上的射影K在直線AE上,當E從D運動到C,則點K所形成軌跡的長度為( )
如圖,在正方形ABCD中,AB=2,E為線段CD上一動點,現將△AED沿AE折起,使點D在面ABC上的射影K在直線AE上,當E從D運動到C,則點K所形成軌跡的長度為( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,3) | B. | $(\root{3}{3},2)$ | C. | $(\root{3}{4},2)$ | D. | $(\root{3}{2},3)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(0,\frac{1}{e})$ | B. | $(-∞,\frac{1}{e})$ | C. | (-∞,-e) | D. | $(\frac{1}{e},+∞)$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com