
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 利用新定義“λ的相關函數”,對①②③④逐個判斷即可得到答案.
解答 解:①、若f(x)為“1一半隨函數”,則f(x+1)+f(x)=0,可得f(x+1)=-f(x),
可得f(x+2)=-f(x+1)=f(x),因此x=0,可得f(0)=f(2);故①正確;
②、假設f(x)=ax是一個“λ一半隨函數”,則ax+λ+λax=0對任意實數x成立,
則有aλ+λ=0,而此式有解,所以f(x)=ax是“λ一半隨函數”,故②正確.
③、令x=0,得f($\frac{1}{2}$)+$\frac{1}{2}$f(0)=0.所以f($\frac{1}{2}$)=-$\frac{1}{2}$f(0),
若f(0)=0,顯然f(x)=0有實數根;若f(0)≠0,f($\frac{1}{2}$)•f(0)=-$\frac{1}{2}$(f(0))2<0,
又因為f(x)的函數圖象是連續不斷,所以f(x)在(0,$\frac{1}{2}$)上必有實數根,
因此任意的“-$\frac{1}{2}$一半隨函數”必有根,即任意“-$\frac{1}{2}$一半隨函數”至少有一個零點.故③正確.
④、假設f(x)=x2是一個“λ一半隨函數”,則(x+λ)2+λx2=0,
即(1+λ)x2+2λx+λ2=0對任意實數x成立,所以λ+1=2λ=λ2=0,而此式無解,所以f(x)=x2不是一個“λ-同伴函數”.故④錯誤
正確判斷:①②③.
故選:C.
點評 本題考查的知識點是函數的概念及構成要素,函數的零點,正確理解f(x)是λ-同伴函數的定義,是解答本題的關鍵.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1-$\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 5-$\sqrt{2}$ | D. | $\sqrt{2}$-5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{5}{3}<a<-\frac{3}{16}$ | B. | $-\frac{8}{5}<a<-\frac{3}{16}$ | C. | $-\frac{8}{3}<a<-\frac{1}{16}$ | D. | $-\frac{6}{5}<a<-\frac{3}{16}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
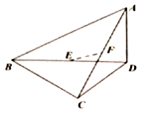 如圖,三棱錐A-BCD中,BC⊥CD,AD⊥平面BCD,E、F分別為BD、AC的中點.
如圖,三棱錐A-BCD中,BC⊥CD,AD⊥平面BCD,E、F分別為BD、AC的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com