Question

9．已知f（x）是定義在R上的增函數，函數y=f（x-1）的圖象關于點（1，0）對稱，若對任意的x，y∈R，等式f（y-3）+f（$\sqrt{4x-{x}^{2}-3}$）=0恒成立，則$\frac{y}{x}$的取值范圍是[2-$\frac{2\sqrt{3}}{3}$.3]．

Answer 1

分析 推導出f（x）為奇函數，y=3-$\sqrt{4x-{x}^{2}-3}$為以（2，3）為圓心，1為半徑的下半圓，從而$\frac{y}{x}$可看作是半圓上的點與原點的連線的斜率，由此能求出$\frac{y}{x}$的取值范圍．

解答 解：函數y=f（x）的圖象可由y=f（x-1）的圖象向左平移1個單位得到，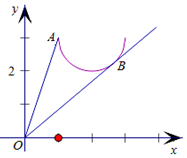
由于y=f（x-1）的圖象關于點（1，0）對稱，則y=f（x）的圖象關于原點對稱，
則f（x）為奇函數，即有f（-x）=-f（x），
則等式f（y-3）+f（$\sqrt{4x-{x}^{2}-3}$）=0恒成立，
即為f（y-3）=-f（$\sqrt{4x-{x}^{2}-3}$）=f（-$\sqrt{4x-{x}^{2}-3}$），
又f（x）是定義在R上的增函數，則有y-3=-$\sqrt{4x-{x}^{2}-3}$，
兩邊平方可得，（x-2）²+（y-3）²=1，
即有y=3-$\sqrt{4x-{x}^{2}-3}$為以（2，3）為圓心，1為半徑的下半圓，
則$\frac{y}{x}$=$\frac{y-0}{x-0}$，可看作是半圓上的點與原點的連線的斜率，
如圖，k_OA=$\frac{3-0}{1-0}$=3，取得最大，過O作切線OB，設OB：y=kx，
則由d=r得，$\frac{|2k-3|}{\sqrt{1+{k}^{2}}}$=1，解得，k=2±$\frac{2\sqrt{3}}{3}$，
由于切點在下半圓，則取k=2-$\frac{2\sqrt{3}}{3}$，即為最小值．則$\frac{y}{x}$的取值范圍是$[{2-\frac{{2\sqrt{3}}}{3}，3}]$．
故答案為：$[{2-\frac{{2\sqrt{3}}}{3}，3}]$．

點評 本題考查代數式的取值范圍的求法，是中檔題，解題時要認真審題，注意函數性質的合理運用．