Question

17．關于函數f（x）=xln|x|的五個命題：
①f（x）在區間（-∞，-$\frac{1}{e}$）上是單調遞增函數；
②f（x）只有極小值點，沒有極大值點；
③f（x）＞0的解集是（-1，0）∪（0，1）；
④函數f（x）在x=1處的切線方程為x-y+1=0；
⑤函數g（x）=f（x）-m最多有2個零點．
其中，是真命題的有①（請把真命題的序號填在橫線上）．

Answer 1

分析 當x＞0時，可得f（x）=xlnx的導數為f′（x）=1+lnx，可得f（x）在（0，$\frac{1}{e}$）遞減；在（$\frac{1}{e}$，+∞）遞增．可得f（x）在x=$\frac{1}{e}$處取得極小值-$\frac{1}{e}$
又∵函數f（x）=xln|x|為奇函數，故其圖象如下，根據圖象可判定①②③⑤；
④，求得x=1處的切線的斜率和切點，由點斜式方程，可得切線方程，即可判斷；

解答 解：當x＞0時，可得f（x）=xlnx的導數為f′（x）=1+lnx，
可得f（x）在（0，$\frac{1}{e}$）遞減；在（$\frac{1}{e}$，+∞）遞增．可得f（x）在x=$\frac{1}{e}$處取得極小值-$\frac{1}{e}$
又∵函數f（x）=xln|x|為奇函數，故其圖象如下：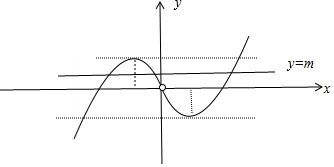

根據圖象
對于①，f（x）在區間（-∞，-$\frac{1}{e}$）上是單調遞增函數，故①正確；
對于②，f（x）有極小值點，有極大值點，故②錯；
對于③，f（x）＞0的解集是（-1，0）∪（1，+∞），故③錯；
對于④，函數f（x）在x=1處的切線斜率為1，切點為（1，0），即有切線的方程為y=x-1，故④錯；
對于⑤，函數g（x）=f（x）-m最多有3個零點，故錯；
故答案為：①

點評 本題考查導數的運用：求切線的方程和單調區間、極值，同時考查函數的零點的個數，注意運用轉化思想、數形結合思想，屬于中檔題．