
分析 (1)求出函數的導數,解關于導函數的不等式,問題轉化為$a≥{({\frac{1+x}{{{x^2}+2x+2}}})_{max}}$,根據函數的單調性求出a的范圍即可;
(2)取a=$\frac{1}{2}$,根據$ln({1+x})<\frac{1}{2}•\frac{{{x^2}+2x}}{1+x}$對x∈(0,+∞),均成立,令$x=\frac{k}{n^2}({k=1,2,…,n})$,作和證出結論即可.
解答 (1)解:函數h(x)的定義域為(-1,+∞),
且$h(x)=f(x)-g(x)=ln({1+x})-a•\frac{{{x^2}+2x}}{1+x}$,
則$h'(x)=\frac{1}{1+x}-a•\frac{{({2x+2})({1+x})-({{x^2}+2x})}}{{({1+{x^2}})}}=\frac{{({1+x})-a•({{x^2}+2x+2})}}{{({1+{x^2}})}}$,
由于h(x)在(-1,+∞)內單調遞減,
則h'(x)≤0對x∈(-1,+∞)恒成立,
即(1+x)-a•(x2+2x+2)≤0對x∈(-1,+∞)恒成立,…(2分)
從而$a≥{({\frac{1+x}{{{x^2}+2x+2}}})_{max}}$,則$a≥{({\frac{1}{{1+x+\frac{1}{1+x}}}})_{max}}=\frac{1}{2}$,
故a的取值范圍為$[{\frac{1}{2},+∞})$…(4分)
(2)證明:取$a=\frac{1}{2}$,由第(1)問可知h(x)在(0,+∞)為單調遞減函數,
從而h(x)<h(0)=0;
則$ln({1+x})<\frac{1}{2}•\frac{{{x^2}+2x}}{1+x}$對x∈(0,+∞),均成立,…(6分)
令$x=\frac{k}{n^2}({k=1,2,…,n})$,
有$ln({1+\frac{k}{n^2}})<\frac{1}{2}•\frac{{{{({\frac{k}{n^2}})}^2}+2•\frac{k}{n^2}}}{{1+\frac{k}{n^2}}}=\frac{1}{2}({\frac{k}{n^2}+\frac{k}{{{n^2}+k}}})≤\frac{1}{2}({\frac{k}{n^2}+\frac{k}{{{n^2}+1}}})$;…(9分)
從而$ln[{({1+\frac{1}{n^2}})({1+\frac{2}{n^2}})…({1+\frac{n}{n^2}})}]$
=$ln({1+\frac{1}{n^2}})+ln({1+\frac{2}{n^2}})+…+ln({1+\frac{n}{n^2}})<\frac{1}{2}({\frac{1}{n^2}+\frac{2}{n^2}+…+\frac{n}{n^2}+\frac{1}{{{n^2}+1}}+\frac{2}{{{n^2}+1}}+…+\frac{n}{{{n^2}+1}}})$
=$\frac{1}{4}[{3-\frac{{n{{({n-1})}^2}+({n-1})}}{{n({{n^2}+1})}}}]≤\frac{3}{4}$,
故$({1+\frac{1}{n^2}})({1+\frac{2}{n^2}})…({1+\frac{n}{n^2}})<{e^{\frac{3}{4}}}$…(12分)
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及不等式的證明,是一道綜合題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | -21 | B. | -32 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 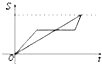 | B. | 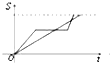 | C. |  | D. |  |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[e-\frac{1}{e},e)$ | B. | [1,e+1) | C. | [e,e+1) | D. | $(e-\frac{1}{e},e+1)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | 2.7歲 | B. | 3.1歲 | C. | 3.2歲 | D. | 4歲 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com