
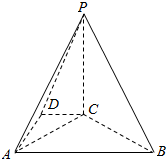
 在四棱錐P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2$\sqrt{3}$,∠CBA=30°.
在四棱錐P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2$\sqrt{3}$,∠CBA=30°.分析 (1)推導出PC⊥AC,AC=2,從而AC⊥BC,進而AC⊥平面PBC,由此能證明AC⊥PB.
(2)以C為原點,CA為x軸,CB為y軸,CP為z軸,建立空間直角坐標系,利用向量法能求出BM的值.
解答 證明:(1)∵PC⊥平面ABCD,∴PC⊥AC,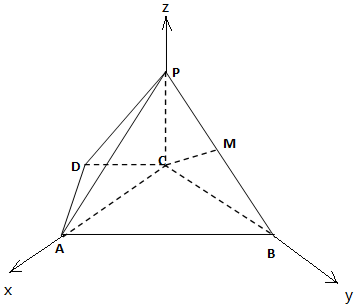
又∠CBA=30°,BC=2$\sqrt{3}$,AB=4,
∴AC=$\sqrt{A{B^2}+B{C^2}-2AB•BCcos∠CBA}$
=$\sqrt{16+12-2×4×2\sqrt{3}×\frac{{\sqrt{3}}}{2}}=2$,
∴AC2+BC2=4+12=16=AB2,∴∠ACB=90°,
故AC⊥BC.
又∵PC、BC是平面PBC內的兩條相交直線,
∴AC⊥平面PBC,∴AC⊥PB. 7分
解:(2)以C為原點,CA為x軸,CB為y軸,CP為z軸,建立空間直角坐標系,
B(0,2$\sqrt{3}$,0),A(2,0,0),P(0,0,2),D(1,-$\sqrt{3}$,0),
設M(0,b,c),$\overrightarrow{PM}=λ\overrightarrow{PB}$,(0≤λ≤1),即(0,b,c-2)=(0,2$\sqrt{3}λ$,-2λ),
∴b=2$\sqrt{2}λ$,c=2-2λ.M(0,2$\sqrt{2}λ$,2-2λ),∴$\overrightarrow{CM}$=(0,2$\sqrt{3}$λ,2-2λ),
設平面PAD的法向量$\overrightarrow{m}$=(x,y,z),
則$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PA}=2x-2z=0}\\{\overrightarrow{m}•\overrightarrow{PD}=x-\sqrt{3}y-2z=0}\end{array}\right.$,取x=1,得$\overrightarrow{m}$=(1,-$\frac{\sqrt{3}}{3}$,1)
∵CM∥平面PAD,
∴$\overrightarrow{CM}$•$\overrightarrow{m}$=-2λ+2-2λ=0,解得λ=$\frac{1}{2}$,
∴M(0,$\sqrt{3}$,1),
∴BM=$\sqrt{(2\sqrt{3}-\sqrt{3})^{2}+(0-1)^{2}}$=2.14分
點評 本題考查線線垂直的證明,考查線段長的求法,是中檔題,解題時要認真審題,注意向量法的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | -$\frac{5}{13}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{2}-1$ | B. | $2\sqrt{2}+1$ | C. | $2\sqrt{2}+2$ | D. | $2\sqrt{2}-2$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com