
分析 (Ⅰ)利用輔助角公式化簡,將已知函數解析式轉化為正弦函數,根據正弦函數圖象解答;
(Ⅱ)首項求得g(x)=2sin(2x+$\frac{π}{6}$),利用正弦函數圖象解題.
解答 解:(Ⅰ)f(x)=sinx+$\sqrt{3}$cosx=2sin(x+$\frac{π}{3}$).
由2kπ-$\frac{π}{2}$≤x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$(k∈Z)
得:2kπ-$\frac{5π}{6}$≤x≤2kπ+$\frac{π}{6}$(k∈Z),故f(x)的單調遞增區間是:[2kπ-$\frac{5π}{6}$,2kπ+$\frac{π}{6}$],k∈Z.
(Ⅱ)g(x)=[f(x)]2-2,
=4sin2(x+$\frac{π}{3}$)-2,
=4×$\frac{1}{2}$[1-cos(2x+$\frac{2π}{3}$)]-2,
=-2cos(2x+$\frac{2π}{3}$),
=2sin(2x+$\frac{π}{6}$).
∵x∈[0,$\frac{π}{4}$],
∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],
∴g(x)=2sin(2x+$\frac{π}{6}$)的最大值是1,最小值是-2.
點評 本題考查三角函數中的恒等變換應用,正弦函數圖象.利用三角函數公式將函數進行化簡是解決本題的關鍵.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:解答題
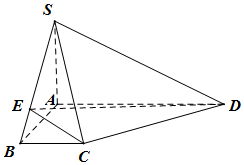 在如圖所示的四棱錐S-ABCD中,SA⊥底面ABCD,∠DAB=∠ABC=90°,SA=AB=BC=a,AD=3a(a>0),E為線段BS上的一個動點.
在如圖所示的四棱錐S-ABCD中,SA⊥底面ABCD,∠DAB=∠ABC=90°,SA=AB=BC=a,AD=3a(a>0),E為線段BS上的一個動點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{9}{5}$ | B. | $\frac{12}{5}$ | C. | $\frac{18}{5}$ | D. | $\frac{24}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
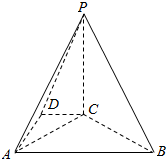 在四棱錐P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2$\sqrt{3}$,∠CBA=30°.
在四棱錐P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2$\sqrt{3}$,∠CBA=30°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com