
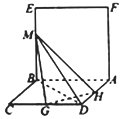
 如圖,已知平面ABEF⊥平面ABCD,四邊形ABEF是正方形,四邊形ABCD是菱形,且BC=2,∠BAD=60°,點G,H分別為邊CD,DA的中點,點M是線段BE上的動點.
如圖,已知平面ABEF⊥平面ABCD,四邊形ABEF是正方形,四邊形ABCD是菱形,且BC=2,∠BAD=60°,點G,H分別為邊CD,DA的中點,點M是線段BE上的動點.分析 (Ⅰ)連接AC交BD于點O.則BE⊥AB.再由已知結合面面垂直的性質可得BE⊥平面ABCD,進一步得到BE⊥AC.由四邊形ABCD為菱形,得BD⊥AC.由面面垂直的判定可得AC⊥平面BDM.由三角形中位線定理得GH∥AC,則GH⊥平面BDM;
(Ⅱ)在菱形ABCD中,利用正弦定理求得三角形DGM的面積,由圖可得當點M與點E重合時,BM取最大值2,代入三棱錐體積公式求得三棱錐D-MGH的體積的最大值.
解答 (Ⅰ)證明:連接AC交BD于點O.
∵四邊形ABEF為正方形.∴BE⊥AB.
又∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB.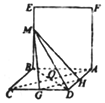
∴BE⊥平面ABCD.
又AC?平面ABCD,∴BE⊥AC.
∵四邊形ABCD為菱形,∴BD⊥AC.
∵BD∩BE=B,∴AC⊥平面BDE,即AC⊥平面BDM.
∵G、H分別為DC、AD的中點,∴GH∥AC,
∴GH⊥平面BDM;
(Ⅱ)解:在菱形ABCD中,
由∠BAD=60°,得∠ADC=120°.
又∵DG=DH=1,∴${S}_{△DGM}=\frac{1}{2}DG•DH•sin120°=\frac{1}{2}×1×1×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$.
∵BE⊥平面ABCD,即BM⊥平面ABCD,
∴${V}_{D-MGH}={V}_{M-DGH}=\frac{1}{3}{S}_{△DGH}•BM=\frac{\sqrt{3}}{12}BM$.
顯然,當點M與點E重合時,BM取最大值2,
此時$({V}_{D-MGH})_{MAX}=\frac{\sqrt{3}}{12}×2=\frac{\sqrt{3}}{6}$,
即三棱錐D-MGH的體積的最大值為$\frac{\sqrt{3}}{6}$.
點評 本題考查直線與平面垂直的判定,考查空間想象能力和思維能力,訓練了利用等積法求多面體的體積,是中檔題.


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:高中數學 來源: 題型:解答題
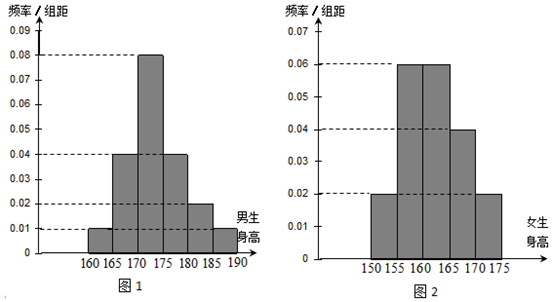
| ≥170cm | <170cm | 總計 | |
| 男生身高 | |||
| 女生身高 | |||
| 總計 |
| P(K2≥k0) | 0.025 | 0.610 | 0.005 | 0.001 |
| k0 | 5.024 | 4.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
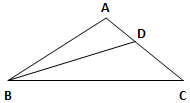 在△ABC中,內角A,B,C所對的邊分別為a,b,c且2a cosC-c=2b.
在△ABC中,內角A,B,C所對的邊分別為a,b,c且2a cosC-c=2b.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com