
分析 利用當$∠AOB=\frac{π}{2}$時,S△AOB面積最大,此時O到AB的距離$d=\sqrt{2}$,即可得出結論.
解答 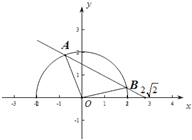 解:如圖:∵${S_{△AOB}}=\frac{1}{2}|{OA}||{OB}|sin∠AOB$=$\frac{1}{2}sin∠AOB≤\frac{1}{2}$,
解:如圖:∵${S_{△AOB}}=\frac{1}{2}|{OA}||{OB}|sin∠AOB$=$\frac{1}{2}sin∠AOB≤\frac{1}{2}$,
當$∠AOB=\frac{π}{2}$時,S△AOB面積最大.此時O到AB的距離$d=\sqrt{2}$.
設AB方程為$y=k(x-2\sqrt{2})({k<0})$,即$kx-y-2\sqrt{2}k=0$.
由$d=\frac{{|{2\sqrt{2}k}|}}{{\sqrt{{k^2}+1}}}=\sqrt{2}$得$k=-\frac{{\sqrt{3}}}{3}$.
故答案為:-$\frac{\sqrt{3}}{3}$.
點評 本題考查三角形面積的計算,考查點到直線的距離公式,考查數形結合的數學思想,屬于中檔題.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:填空題
 高為4的直三棱柱被削去一部分后得到一個幾何體,它的直觀圖和三視圖中的側視圖、俯視圖如圖所示,則該幾何體的體積是原直三棱柱的體積的$\frac{1}{4}$.
高為4的直三棱柱被削去一部分后得到一個幾何體,它的直觀圖和三視圖中的側視圖、俯視圖如圖所示,則該幾何體的體積是原直三棱柱的體積的$\frac{1}{4}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(5,-\frac{4π}{3})$ | B. | $(5,\frac{π}{3})$ | C. | $(5,\frac{2π}{3})$ | D. | $(5,\frac{5π}{3})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
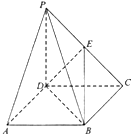 在如圖所示的四棱錐P-ABCD中,底面ABCD為矩形,側棱PD⊥底面ABCD,且PD=CD=2,點E為PC的中點,連接DE,BD,BE.
在如圖所示的四棱錐P-ABCD中,底面ABCD為矩形,側棱PD⊥底面ABCD,且PD=CD=2,點E為PC的中點,連接DE,BD,BE.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com