
分析 (1)求出函數的定義域,求出導函數,令導函數大于0,求出x的范圍,寫出區間形式即得到函數f(x)的單調增區間.
(2)求出導函數,令導函數為0求出根,通過討論根與區間[1,e]的關系,判斷出函數的單調性,求出函數的最小值.
解答 解:f(x)的定義域為x>0
(1)將a=1代入f(x)得f(x)=x2-3x+lnx
所以f′(x)=$\frac{2{x}^{2}-3x+1}{x}$
令f′(x)>0得0<x<$\frac{1}{2}$或x>1
所以函數的單調增區間(0,$\frac{1}{2}$),(1,+∞);
(2)f′(x)=$\frac{2{x}^{2}-(2a+1)+a}{x}$
令f′(x)=0得x=$\frac{1}{2}$(舍)或x=a,
當a≤1時,在區間[1,e]上,f′(x)>0
f(x)在區間[1,e]上的單調遞增
所以[f(x)]min=f(1)=-2a;
當1<a<e時,f(x)在[1,a]單調遞減,在[a,e]上單調遞增
所以[f(x)]min=f(a)=-a2-a+alna;
當a≥e時,f(x)在[1,e]上單調遞減
所以[f(x)]min=f(e)=e2-2ae-e+a.
點評 本題考查了導數和函數的單調性和最值關系,熟練掌握利用導數研究函數的單調性、等價轉化、二次函數的性質等是解題的關鍵,屬于中檔題.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
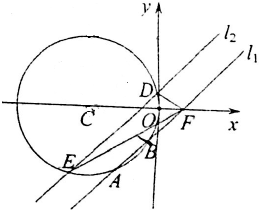 已知直線l1:y=x-1與圓C:(x+a)2+y2=a2(a>0)相交于A、B兩點,|AB|=2,直線l2∥l1,直線l2與圓C相交于D、E兩點.
已知直線l1:y=x-1與圓C:(x+a)2+y2=a2(a>0)相交于A、B兩點,|AB|=2,直線l2∥l1,直線l2與圓C相交于D、E兩點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com