Question

9．如圖，直三棱柱ABC-A₁B₁C₁中，底面是等腰直角三角形，AB=BC=$\sqrt{2}$，BB₁=3，D為A₁C₁的中點，F在線段AA₁上．
（1）AF為何值時，CF與平面B₁DF所成的角為直角？
（2）設AF=1，求平面B₁CF與平面ABC所成的 銳二面角的余弦值．

Answer 1

分析 （1）先證明B₁D⊥平面ACC₁A₁，得出B₁D⊥CF，于是當CF⊥DF時，CF⊥平面B₁DF，利用勾股定理求出AF即可；
（2）建立坐標系，求出平面B₁CF和平面ABC的法向量，計算法向量的夾角即可得出二面角的大小．

解答 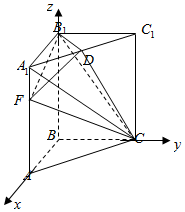解：（1）∵A₁B₁=B₁C₁，D是A₁C₁的中點，
∴B₁D⊥A₁C₁，
∵AA₁⊥平面A₁B₁C₁，B₁D?平面A₁B₁C₁，
∴AA₁⊥B₁D，
又AA₁∩A₁C₁=A₁，
∴B₁D⊥平面ACC₁A₁，∵CF?平面ACC₁A₁，
∴B₁D⊥CF，
∴當CF⊥DF時，CF⊥平面B₁DF，
∵△A₁B₁C₁是等邊三角形，A₁B₁=B₁C₁=$\sqrt{2}$，D是A₁C₁的中點，
∴A₁D=C₁D=1，
設AF=x，則DF=$\sqrt{1+（3-x）^{2}}$，CF=$\sqrt{{x}^{2}+4}$，CD=$\sqrt{10}$，
∴1+（3-x）²+x²+4=10，解得x=1或x=2．
∴當AF=1或AF=2時，CF與平面B₁DF所成的角為直角．
（2）以B為原點，以BA，BC，BB₁為坐標軸建立空間直角坐標系，
則F（$\sqrt{2}$，0，1），C（0，$\sqrt{2}$，0），B₁（0，0，3），
∴$\overrightarrow{{B}_{1}C}$=（0，$\sqrt{2}$，-3），$\overrightarrow{{B}_{1}F}$=（$\sqrt{2}$，0，-2），
設平面B₁CF的法向量為$\overrightarrow{n}$=（x，y，z），則$\left\{\begin{array}{l}{\sqrt{2}y-3z=0}\\{\sqrt{2}x-2z=0}\end{array}\right.$，
令z=$\sqrt{2}$得$\overrightarrow{n}$=（2，3，$\sqrt{2}$），
又BB₁⊥平面ABC，∴$\overrightarrow{m}$=（0，0，1）是平面ABC的一個法向量，
∴cos＜$\overrightarrow{m}，\overrightarrow{n}$＞=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{2}}{\sqrt{15}}$=$\frac{\sqrt{30}}{15}$，
∴平面B₁CF與平面ABC所成的 銳二面角的余弦值為$\frac{\sqrt{30}}{15}$．

點評 本題考查了線面垂直的判定，空間向量與空間角的計算，屬于中檔題．